题目内容
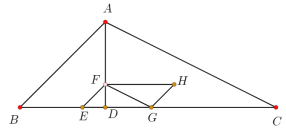
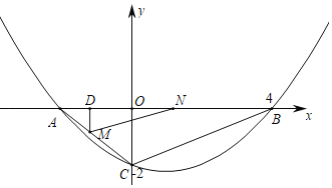
【题目】如图,在等腰Rt△ABC中,AC=BC=6![]() ,∠EDF的顶点D是AB的中点,且∠EDF=45°,现将∠EDF绕点D旋转一周,在旋转过程中,当∠EDF的两边DE、DF分别交直线AC于点G、H,把△DGH沿DH折叠,点G落在点M处,连接AM,若
,∠EDF的顶点D是AB的中点,且∠EDF=45°,现将∠EDF绕点D旋转一周,在旋转过程中,当∠EDF的两边DE、DF分别交直线AC于点G、H,把△DGH沿DH折叠,点G落在点M处,连接AM,若![]() =
=![]() ,则AH的长为_______.
,则AH的长为_______.
【答案】![]() 或
或![]() 或3
或3![]()
【解析】
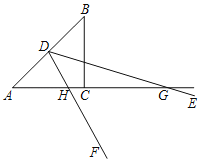
分三种情形:①如图1中,当点H在线段AC上,点G在AC的延长线上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.②如图2中,当点H在线段AC上,点G在上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.③如图3中,当点H在线段CA的延长线上,点G在线段AC上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.首先证明AM⊥AC,利用相似三角形的性质以及勾股定理构建方程解决问题即可.
解:①如图1中,当点H在线段AC上,点G在AC的延长线上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.
∵CA=CB,∠ACB=90°,AD=DB,
∴CD⊥AB,CD=DA=DB,
∴∠ACD=∠DCB=45°,∠DCG=135°,
∵∠EDF=∠EDM=45°,DG=DM,
∴∠ADC=∠MDG,
∴∠ADM=∠CDG,
∴△ADM≌△CDG(SAS),
∴∠DAM=∠DCG=135°,
∵∠CAB=45°,
∴∠CAM=90°,
∴MH=GH=![]() =
=![]() =5k,
=5k,
∵∠GDH=∠GAD=45°,∠DGH=∠AGD,
∴△DGH∽△AGD,
∴![]() =
=![]() ,
,
∴DG2=GHGA=40k2,
∵AC=BC=6![]() ,∠ACB=90°,
,∠ACB=90°,
∴AB=![]() AC=12,
AC=12,
∴AD=CD=6,
∵DJ⊥AC,
∴AJ=JC=3![]() ,DJ=AJ=IC=3
,DJ=AJ=IC=3![]() ,
,
∴GJ=8K﹣3![]() ,
,
在Rt△DJG中,∵DG2=DJ2+GJ2,
∴40k2=(8k﹣3![]() )2+(3
)2+(3![]() )2,
)2,
解得k=![]() 或
或![]() (舍弃),
(舍弃),
∴AH=3k=![]() .
.
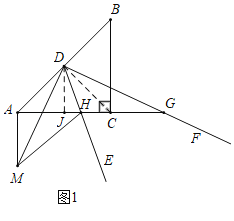
②如图2中,当点H在线段AC上,点G在上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.
同法可得:40k2=(8k﹣3![]() )2+(3
)2+(3![]() )2,
)2,
解得k=![]() (舍弃)或
(舍弃)或![]() ,
,
∴AH=3k=![]() .
.
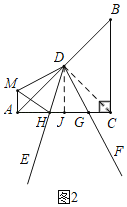
③如图3中,当点H在线段CA的延长线上,点G在线段AC上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.
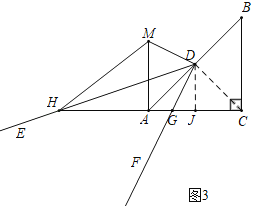
同法可得:10k2=(3![]() ﹣2k)2+(3
﹣2k)2+(3![]() )2,
)2,
解得k=![]() 或﹣3
或﹣3![]() (舍弃),
(舍弃),
∴AH=3k=3![]() ,
,
综上所述,满足条件的AH的值为![]() 或
或![]() 或3
或3![]() .
.
故答案为![]() 或
或![]() 或3
或3![]() .
.