题目内容
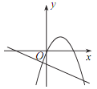
【题目】如图,直线l:y=﹣![]() x+2与x轴、y轴分别交于A、B两点,动点M从点A以每秒1个单位的速度沿x轴向左移动.
x+2与x轴、y轴分别交于A、B两点,动点M从点A以每秒1个单位的速度沿x轴向左移动.
(1)求A、B两点的坐标;
(2)将直线l向上平移4个单位后得到直线l',交y轴于点C.求直线l′的函数表达式;
(3)设点M的移动时间为t,当t为何值时,△COM≌△AOB,并求出此时点M的坐标.
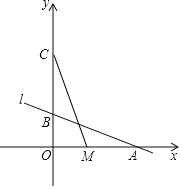
【答案】(1)A(6,0)、B(0,2);(2)![]() ;(3)当t=4或8时,△COM≌△AOB,此时M(2,0)或(﹣2,0).
;(3)当t=4或8时,△COM≌△AOB,此时M(2,0)或(﹣2,0).
【解析】
(1)A和B是坐标轴上的点,求A和B的坐标,只需要令x=0,y=0,即可算出.
(2)向上平移4个单位,就是y轴交点纵坐标向上平移4个单位.平移的函数表达式k不变,利用待定系数法可以求出![]() 得表达式.
得表达式.
(3)![]() 和
和![]() 中,OC=OA=6,
中,OC=OA=6,![]() ,要使
,要使![]() ≌
≌![]() ,只需要OB=OM就行.OB=2,当OM=2时,M在y轴左边时,AM=8,t=8;M在y轴在右边时,AM=4,t=4.
,只需要OB=OM就行.OB=2,当OM=2时,M在y轴左边时,AM=8,t=8;M在y轴在右边时,AM=4,t=4.
解:(1)对于直线l:y=﹣![]() x+2,
x+2,
当x=0时,y=2;当y=0时,x=6,
则A、B两点的坐标分别为A(6,0)、B(0,2);
(2)设直线l′的函数表达式为y=kx+b,
∵l′∥l,
∴k=﹣![]() ,
,
由题意l′经过点(0,6),
∴b=6,
∴l′的函数表达式为![]() ;
;
(3)∵OC=OA=6,∠AOB=∠COM=90°,
∴当点M在OA上时,OB=OM=2,则△COM≌△AOB,
∴AM=AO﹣OM=4,
∴t=4÷1=4,M(2,0).
当M在x轴的负半轴上时,OM=OB=2,△COM≌△AOB,AM=8,
∴t=8÷1=8,点M(﹣2,0).
故当t=4或8时,△COM≌△AOB,此时M(2,0)或(﹣2,0).

练习册系列答案
相关题目