题目内容
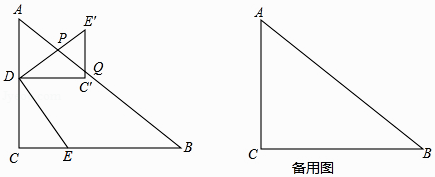
【题目】如图,已知△ABC内接于⊙O,点C在劣弧AB上(不与点A,B重合),点D为弦BC的中点,DE⊥BC,DE与AC的延长线交于点E,射线AO与射线EB交于点F,与⊙O交于点G,设∠GAB=ɑ,∠ACB=β,∠EAG+∠EBA=γ,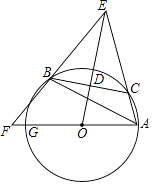
(1)点点同学通过画图和测量得到以下近似数据:
ɑ | 30° | 40° | 50° | 60° |
β | 120° | 130° | 140° | 150° |
γ | 150° | 140° | 130° | 120° |
猜想:β关于ɑ的函数表达式,γ关于ɑ的函数表达式,并给出证明:
(2)若γ=135°,CD=3,△ABE的面积为△ABC的面积的4倍,求⊙O半径的长.
【答案】
(1)
解:β=α+90°,γ=﹣α+180°
连接OB,
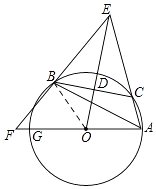
∴由圆周角定理可知:2∠BCA=360°﹣∠BOA,
∵OB=OA,
∴∠OBA=∠OAB=α,
∴∠BOA=180°﹣2α,
∴2β=360°﹣(180°﹣2α),
∴β=α+90°,
∵D是BC的中点,DE⊥BC,
∴OE是线段BC的垂直平分线,
∴BE=CE,∠BED=∠CED,∠EDC=90°
∵∠BCA=∠EDC+∠CED,
∴β=90°+∠CED,
∴∠CED=α,
∴∠CED=∠OBA=α,
∴O、A、E、B四点共圆,
∴∠EBO+∠EAG=180°,
∴∠EBA+∠OBA+∠EAG=180°,
∴γ+α=180°
(2)
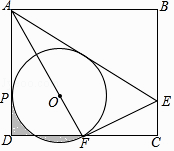
解:当γ=135°时,此时图形如图所示,
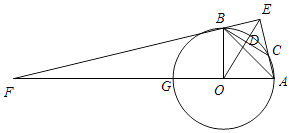
∴α=45°,β=135°,
∴∠BOA=90°,∠BCE=45°,
由(1)可知:O、A、E、B四点共圆,
∴∠BEC=90°,
∵△ABE的面积为△ABC的面积的4倍,
∴ ![]() ,
,
∴ ![]() ,
,
设CE=3x,AC=x,
由(1)可知:BC=2CD=6,
∵∠BCE=45°,
∴CE=BE=3x,
∴由勾股定理可知:(3x)2+(3x)2=62,
x= ![]() ,
,
∴BE=CE=3 ![]() ,AC=
,AC= ![]() ,
,
∴AE=AC+CE=4 ![]() ,
,
在Rt△ABE中,
由勾股定理可知:AB2=(3 ![]() )2+(4
)2+(4 ![]() )2,
)2,
∴AB=5 ![]() ,
,
∵∠BAO=45°,
∴∠AOB=90°,
在Rt△AOB中,设半径为r,
由勾股定理可知:AB2=2r2,
∴r=5,
∴⊙O半径的长为5.
【解析】(1)由圆周角定理即可得出β=α+90°,然后根据D是BC的中点,DE⊥BC,可知∠EDC=90°,由三角形外角的性质即可得出∠CED=α,从而可知O、A、E、B四点共圆,由圆内接四边形的性质可知:∠EBO+∠EAG=180°,即γ=﹣α+180°;(2)由(1)及γ=135°可知∠BOA=90°,∠BCE=45°,∠BEC=90°,由于△ABE的面积为△ABC的面积的4倍,所以 ![]() ,根据勾股定理即可求出AE、AC的长度,从而可求出AB的长度,再由勾股定理即可求出⊙O的半径r;
,根据勾股定理即可求出AE、AC的长度,从而可求出AB的长度,再由勾股定理即可求出⊙O的半径r;
【考点精析】通过灵活运用余角和补角的特征和三角形的面积,掌握互余、互补是指两个角的数量关系,与两个角的位置无关;三角形的面积=1/2×底×高即可以解答此题.

【题目】为了了解某校九年级学生的跳高水平,随机抽取该年级50名学生进行跳高测试,并把测试成绩绘制成如图所示的频数表和未完成的频数直方图(每组含前一个边界值,不含后一个边界值).
某校九年级50名学生跳高测试成绩的频数表
组别(m) | 频数 |
1.09~1.19 | 8 |
1.19~1.29 | 12 |
1.29~1.39 | A |
1.39~1.49 | 10 |
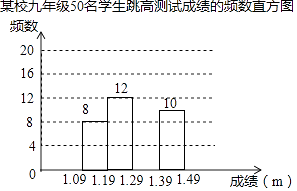
(1)求A的值,并把频数直方图补充完整;
(2)该年级共有500名学生,估计该年级学生跳高成绩在1.29m(含1.29m)以上的人数.