��Ŀ����
����Ŀ��ijУ���꼶10���༶ʦ�����б�ҵ���ջ��ݣ�ÿ��2����Ŀ���и質���赸�����Ŀ���꼶ͳ�ƺ��ֳ������Ŀ�����赸���Ŀ����2����4����
��1�����꼶ʦ�����ݵĸ質���赸���Ŀ�����ж��ٸ���
��2����У�ߡ����꼶ʦ����СƷ��Ŀ���룬�ڸ質���赸��СƷ�����Ŀ�У�ÿ����Ŀ���ݳ�ƽ����ʱ�ֱ���5���ӡ�6���ӡ�8���ӣ�Ԥ�������ݳ���Ŀ������ʱ����15���ӣ�����20��00��ʼ��22��30֮ǰ�ݳ��������ʲ����СƷ���Ŀ������ж��ٸ���
���𰸡�
��1��
�⣺����꼶ʦ�����ݵĸ質���Ŀ��x�����赸���Ŀ��y����
�������⣬�ã� ![]() ����ã�
����ã� ![]() ��
��
�𣺾��꼶ʦ�����ݵĸ質���Ŀ��12�����赸���Ŀ��8����
��2��
�⣺������СƷ���Ŀ��a����
�������⣬�ã�12��5+8��6+8a+15��150��
��ã�a�� ![]() ��
��
����a������
��a=3��
�𣺲����СƷ���Ŀ�������3����
����������1������꼶ʦ�����ݵĸ質���Ŀ��x�����赸���Ŀ��y�������ݡ������Ŀ������Ϊ20�����������Ŀ�����赸���Ŀ����2����4�����з��������ɵã�
��2��������СƷ���Ŀ��a�������ݡ������Ŀ����ʱ��+������ʱ��150���в���ʽ���ɵã�

 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�����Ŀ���� ��1����48��ѧ���μ�ѧУ���еġ���ϧ������Զ�붾Ʒ��ֻ�Ǿ�������������Գɼ����з������������µ�Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ��δ��ɣ�������8��ѧ���ɼ���δͳ�ƣ���8��ѧ���ɼ����£�60��90��63��99��67��99��99��68�� Ƶ���ֲ���
������ | Ƶ���������� |
60��x��70 | a |
70��x��80 | 16 |
80��x��90 | 24 |
90��x��100 | b |

�����������⣺
��1�����Ƶ���ֲ�����a= �� b= ��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3��ȫУ����600��ѧ���μӳ��������Ƹ�У�ɼ�90��x��100��Χ�ڵ�ѧ���ж����ˣ�
��4���� ��1����ס��ҡ�����λͬѧ�ijɼ����е�һ����ѡ���˲μӾ�������ǡ��ѡ�мס�����λͬѧ�ĸ��ʣ�
����Ŀ����ͼ����֪��ABC�ڽ��ڡ�O����C���ӻ�AB�ϣ������A��B�غϣ�����DΪ��BC���е㣬DE��BC��DE��AC���ӳ��߽��ڵ�E������AO������EB���ڵ�F�����O���ڵ�G�����GAB=������ACB=�£���EAG+��EBA=�ã�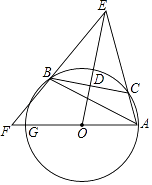
��1�����ͬѧͨ����ͼ�Ͳ����õ����½������ݣ�
�� | 30�� | 40�� | 50�� | 60�� |
�� | 120�� | 130�� | 140�� | 150�� |
�� | 150�� | 140�� | 130�� | 120�� |
���룺�¹��ڨ��ĺ�������ʽ���ù��ڨ��ĺ�������ʽ��������֤����
��2������=135�㣬CD=3����ABE�����Ϊ��ABC�������4�������O�뾶�ij���