题目内容
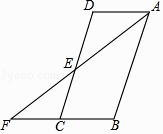
【题目】如图,△ABC内接于⊙O,CD平分∠ACB交⊙O于D,过点D作PQ∥AB分别交CA、CB延长线于P、Q,连接BD. 
(1)求证:PQ是⊙O的切线;
(2)求证:BD2=ACBQ;
(3)若AC、BQ的长是关于x的方程x+ ![]() =m的两实根,且tan∠PCD=
=m的两实根,且tan∠PCD= ![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】
(1)证明:∵PQ∥AB,
∴∠ABD=∠BDQ=∠ACD,
∵∠ACD=∠BCD,
∴∠BDQ=∠ACD,
如图1,连接OB,OD,交AB于E,

则∠OBD=∠ODB,∠O=2∠DCB=2∠BDQ,
在△OBD中,∠OBD+∠ODB+∠O=180°,
∴2∠ODB+2∠O=180°,
∴∠ODB+∠O=90°,
∴PQ是⊙O的切线
(2)证明:如图2,连接AD,

由(1)知PQ是⊙O的切线,
∴∠BDQ=∠DCB=∠ACD=∠BCD=∠BAD,
∴AD=BD,
∵∠DBQ=∠ACD,
∴△BDQ∽△ACD,
∴ ![]() =
= ![]() ,
,
∴BD2=ACBQ
(3)解:方程x+ ![]() =m可化为x2﹣mx+4=0,
=m可化为x2﹣mx+4=0,
∵AC、BQ的长是关于x的方程x+ ![]() =m的两实根,
=m的两实根,
∴ACBQ=4,由(2)得BD2=ACBQ,
∴BD2=4,
∴BD=2,
由(1)知PQ是⊙O的切线,
∴OD⊥PQ,
∵PQ∥AB,
∴OD⊥AB,由(1)得∠PCD=∠ABD,
∵tan∠PCD= ![]() ,
,
∴tan∠ABD= ![]() ,
,
∴BE=3DE,
∴DE2+(3DE)2=BD2=4,
∴DE= ![]() ,
,
∴BE= ![]() ,
,
设OB=OD=R,
∴OE=R﹣ ![]() ,
,
∵OB2=OE2+BE2,
∴R2=(R﹣ ![]() )2+(
)2+( ![]() )2,
)2,
解得:R=2 ![]() ,
,
∴⊙O的半径为2 ![]()
【解析】(1)根据平行线的性质和圆周角定理得到∠ABD=∠BDQ=∠ACD,连接OB,OD,交AB于E,根据圆周角定理得到∠OBD=∠ODB,∠O=2∠DCB=2∠BDQ,根据三角形的内角和得到2∠ODB+2∠O=180°,于是得到∠ODB+∠O=90°,根据切线的判定定理即可得到结论;(2)证明:连接AD,根据等腰三角形的判定得到AD=BD,根据相似三角形的性质即可得到结论;(3)根据题意得到ACBQ=4,得到BD=2,由(1)知PQ是⊙O的切线,由切线的性质得到OD⊥PQ,根据平行线的性质得到OD⊥AB,根据三角函数的定义得到BE=3DE,根据勾股定理得到BE= ![]() ,设OB=OD=R,根据勾股定理即可得到结论.
,设OB=OD=R,根据勾股定理即可得到结论.
【考点精析】关于本题考查的分式方程的解和圆周角定理,需要了解分式方程无解(转化成整式方程来解,产生了增根;转化的整式方程无解);解的正负情况:先化为整式方程,求整式方程的解;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能得出正确答案.

【题目】如图,已知△ABC内接于⊙O,点C在劣弧AB上(不与点A,B重合),点D为弦BC的中点,DE⊥BC,DE与AC的延长线交于点E,射线AO与射线EB交于点F,与⊙O交于点G,设∠GAB=ɑ,∠ACB=β,∠EAG+∠EBA=γ,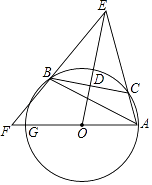
(1)点点同学通过画图和测量得到以下近似数据:
ɑ | 30° | 40° | 50° | 60° |
β | 120° | 130° | 140° | 150° |
γ | 150° | 140° | 130° | 120° |
猜想:β关于ɑ的函数表达式,γ关于ɑ的函数表达式,并给出证明:
(2)若γ=135°,CD=3,△ABE的面积为△ABC的面积的4倍,求⊙O半径的长.