题目内容
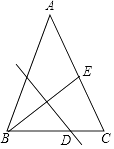
【题目】如图，矩形ABCD中，E是BC上一点，连接AE，将矩形沿AE翻折，使点B落在CD边F处，连接AF，在AF上取点O，以O为圆心，OF长为半径作⊙O与AD相切于点P．若AB=6，BC=3 
，则下列结论：①F是CD的中点；②⊙O的半径是2；③AE= 
CE；④S阴影= 
．其中正确结论的序号是 ． 
【答案】①②④
【解析】解：①∵AF是AB翻折而来，∴AF=AB=6，
∵AD=BC=3 
，∴DF= 
=3，
∴F是CD中点；∴①正确；②连接OP，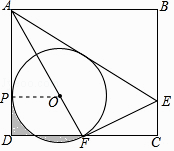
∵⊙O与AD相切于点P，∴OP⊥AD，
∵AD⊥DC，∴OP∥CD，
∴ 
= 
，
设OP=OF=x，则 
= 
，解得：x=2，
∴②正确；③∵RT△ADF中，AF=6，DF=3，
∴∠DAF=30°，∠AFD=60°，
∴∠EAF=∠EAB=30°，
∴AE=2EF；
∵∠AFE=90°，
∴∠EFC=90°﹣∠AFD=30°，
∴EF=2EC，
∴AE=4CE，∴③错误；
④连接OG，作OH⊥FG，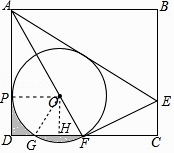
∵∠AFD=60°，OF=OG，∴△OFG为等边△；同理△OPG为等边△；
∴∠POG=∠FOG=60°，OH= 
OG= ，S扇形OPG=S扇形OGF ，
∴S阴影=（S矩形OPDH﹣S扇形OPG﹣S△OGH）+（S扇形OGF﹣S△OFG）
=S矩形OPDH﹣ 
S△OFG=2× ﹣ （ 
×2× ）= ．∴④正确；
所以答案是①②④．
【考点精析】认真审题，首先需要了解矩形的性质(矩形的四个角都是直角，矩形的对角线相等)，还要掌握切线的性质定理(切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径)的相关知识才是答题的关键．
【题目】九 （1）班48名学生参加学校举行的“珍惜生命，远离毒品”只是竞赛初赛，赛后，班长对成绩进行分析，制作如下的频数分布表和频数分布直方图（未完成）．余下8名学生成绩尚未统计，这8名学生成绩如下：60，90，63，99，67，99，99，68． 频数分布表
分数段 | 频数（人数） |
60≤x＜70 | a |
70≤x＜80 | 16 |
80≤x＜90 | 24 |
90≤x＜100 | b |
请解答下列问题：
（1）完成频数分布表，a= ， b= ．
（2）补全频数分布直方图；
（3）全校共有600名学生参加初赛，估计该校成绩90≤x＜100范围内的学生有多少人？
（4）九 （1）班甲、乙、丙三位同学的成绩并列第一，现选两人参加决赛，求恰好选中甲、乙两位同学的概率．
【题目】如图，已知△ABC内接于⊙O，点C在劣弧AB上（不与点A，B重合），点D为弦BC的中点，DE⊥BC，DE与AC的延长线交于点E，射线AO与射线EB交于点F，与⊙O交于点G，设∠GAB=ɑ，∠ACB=β，∠EAG+∠EBA=γ，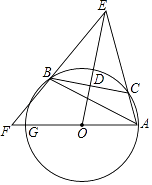
（1）点点同学通过画图和测量得到以下近似数据：
ɑ | 30° | 40° | 50° | 60° |
β | 120° | 130° | 140° | 150° |
γ | 150° | 140° | 130° | 120° |
猜想：β关于ɑ的函数表达式，γ关于ɑ的函数表达式，并给出证明：
（2）若γ=135°，CD=3，△ABE的面积为△ABC的面积的4倍，求⊙O半径的长．
