题目内容
【题目】如图，在矩形ABCD中，AB= 
，E是BC的中点，AE⊥BD于点F，则CF的长是 ． 
【答案】
【解析】解：∵四边形ABCD是矩形， ∴∠ABE=∠BAD=90°，
∵AE⊥BD，
∴∠AFB=90°，
∴∠BAF+∠ABD=∠ABD+∠ADB=90°，
∴∠BAE=∠ADB，
∴△ABE∽△ADB，
∴ 
，
∵E是BC的中点，
∴AD=2BE，
∴2BE2=AB2=2，
∴BE=1，
∴BC=2，
∴AE= 
= 
，BD= 
= 
，
∴BF= 
= 
，
过F作FG⊥BC于G，
∴FG∥CD，
∴△BFG∽△BDC，
∴ 
= 
= 
，
∴FG= 
，BG= 
，
∴CG= 
，
∴CF= 
= ．
所以答案是： ．
【考点精析】解答此题的关键在于理解矩形的性质的相关知识，掌握矩形的四个角都是直角，矩形的对角线相等．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】九 （1）班48名学生参加学校举行的“珍惜生命，远离毒品”只是竞赛初赛，赛后，班长对成绩进行分析，制作如下的频数分布表和频数分布直方图（未完成）．余下8名学生成绩尚未统计，这8名学生成绩如下：60，90，63，99，67，99，99，68． 频数分布表
分数段 | 频数（人数） |
60≤x＜70 | a |
70≤x＜80 | 16 |
80≤x＜90 | 24 |
90≤x＜100 | b |
请解答下列问题：
（1）完成频数分布表，a= ， b= ．
（2）补全频数分布直方图；
（3）全校共有600名学生参加初赛，估计该校成绩90≤x＜100范围内的学生有多少人？
（4）九 （1）班甲、乙、丙三位同学的成绩并列第一，现选两人参加决赛，求恰好选中甲、乙两位同学的概率．
【题目】如图，已知△ABC内接于⊙O，点C在劣弧AB上（不与点A，B重合），点D为弦BC的中点，DE⊥BC，DE与AC的延长线交于点E，射线AO与射线EB交于点F，与⊙O交于点G，设∠GAB=ɑ，∠ACB=β，∠EAG+∠EBA=γ，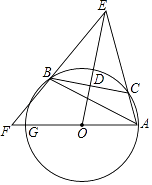
（1）点点同学通过画图和测量得到以下近似数据：
ɑ | 30° | 40° | 50° | 60° |
β | 120° | 130° | 140° | 150° |
γ | 150° | 140° | 130° | 120° |
猜想：β关于ɑ的函数表达式，γ关于ɑ的函数表达式，并给出证明：
（2）若γ=135°，CD=3，△ABE的面积为△ABC的面积的4倍，求⊙O半径的长．
