题目内容
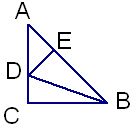
在直角△ABC中,∠C=90º,AC=BC,BD平分∠ABC,DE⊥AB于E,若CD=3,则AD的长度是( )

| A.3 | B.4 | C.2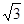 | D.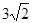 |
D
试题分析:先证得△BCD≌△BED,即得ED=CD=3,由∠C=90º,AC=BC,可得∠A=45º,再有DE⊥AB,可得△ADE为等腰直角三角形,即可求得结果.
∵BD平分∠ABC,
∴∠EBD=∠CBD,
∵∠C=90º,DE⊥AB,BD=BD,
∴△BCD≌△BED,
∴ED=CD=3,
∵∠C=90º,AC=BC,
∴∠A=45º,
∵DE⊥AB,
∴△ADE为等腰直角三角形,
∴AE=ED=3,
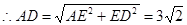 ,
,故选D.
点评:本题属于基础应用题,只需学生熟练掌握等腰直角三角形的判定和性质,即可完成.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
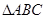 中,点
中,点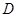 为
为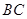 边上的一点,
边上的一点,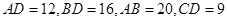 .
.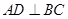 .
.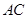 的长及
的长及
 的距离是()
的距离是()