题目内容
【题目】已知一次函数y=![]() 的图象是直线l1, ,l1与y轴相交于点A,与x轴相交于点B,直线l2经过点B,并且与y轴相交于点C,点C到原点的距离是6个单位长度。
的图象是直线l1, ,l1与y轴相交于点A,与x轴相交于点B,直线l2经过点B,并且与y轴相交于点C,点C到原点的距离是6个单位长度。
(1)求直线l2所对应的一次函数表达式;
(2)求△ABC形的面积.
【答案】(1)y=-![]() x+5或y=
x+5或y=![]() x-5;
x-5;
(2)△ABC的面积为24或6.
【解析】
试题分析:先求出点A、B的坐标,然后分点C在y轴正半轴与负半轴两种情况写出点C的坐标,再利用待定系数法求直线解析式即可.根据C的坐标求△ABC的面积即可.
试题解析:(1)令x=0,则y=![]() ×0-3=-3,
×0-3=-3,
令y=0,则![]() x-3=0,解得x=6,
x-3=0,解得x=6,
所以,点A(0,-3),B(6,0),
∵y轴上的点C到原点的距离是5个单位,
∴点C的坐标为(0,5),(0,-5),
设直线L2的解析式为y=kx+b,
则![]() 或
或![]() ,
,
解得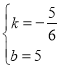 或
或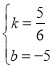 ,
,
所以直线L2所对应的一次函数关系式为y=-![]() x+5或y=
x+5或y=![]() x-5;
x-5;
(2)点C的坐标为(0,5)时,AC=8,
△ABC的面积=![]() ×8×6=24,
×8×6=24,
点C的坐标为(0,-5)时,AC=2,
△ABC的面积=![]() ×2×6=6.
×2×6=6.
故△ABC的面积为24或6.

练习册系列答案
相关题目