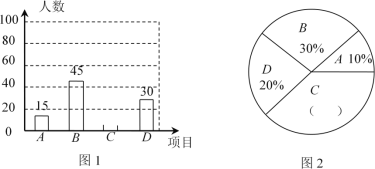
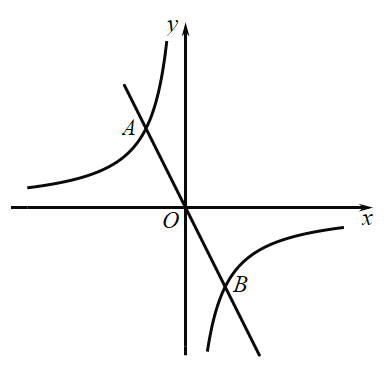
题目内容
【题目】为倡导健康环保,自带水杯已成为一种好习惯,某超市销售甲,乙两种型号水杯,进价和售价均保持不变,其中甲种型号水杯进价为25元/个,乙种型号水杯进价为45元/个,下表是前两月两种型号水杯的销售情况:
时间 | 销售数量(个) | 销售收入(元)(销售收入=售价×销售数量) | |
甲种型号 | 乙种型号 | ||
第一月 | 22 | 8 | 1100 |
第二月 | 38 | 24 | 2460 |
(1)求甲、乙两种型号水杯的售价;
(2)第三月超市计划再购进甲、乙两种型号水杯共80个,这批水杯进货的预算成本不超过2600元,且甲种型号水杯最多购进55个,在80个水杯全部售完的情况下设购进甲种号水杯a个,利润为w元,写出w与a的函数关系式,并求出第三月的最大利润.
【答案】(1)甲、乙两种型号水杯的销售单价分别为30元、55元;(2)w=﹣5a+800,第三月的最大利润为550元.
【解析】
(1)设甲种型号的水杯的售价为每个![]() 元,乙种型号的水杯每个
元,乙种型号的水杯每个![]() 元,根据题意列出方程组求解即可,
元,根据题意列出方程组求解即可,
(2)根据题意写出利润![]() 关于
关于![]() 的一次函数关系式,列不等式组求解
的一次函数关系式,列不等式组求解![]() 的范围,从而利用一次函数的性质求利润的最大值.
的范围,从而利用一次函数的性质求利润的最大值.
解:(1)设甲种型号的水杯的售价为每个![]() 元,乙种型号的水杯每个
元,乙种型号的水杯每个![]() 元,则
元,则
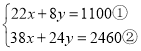
①![]() ②得:
②得:![]()
![]()
把![]() 代入①得:
代入①得:![]()
![]()
答:甲、乙两种型号水杯的销售单价分别为30元、55元;
(2)由题意得:甲种水杯进了![]() 个,则乙种水杯进了
个,则乙种水杯进了![]() 个,
个,
所以:![]()
又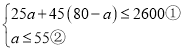
由①得:![]() ,
,
所以不等式组的解集为:![]()
其中![]() 为正整数,所以
为正整数,所以![]()
![]()
![]() 随
随![]() 的增大而减小,
的增大而减小,
当![]() 时,第三月利润达到最大,最大利润为:
时,第三月利润达到最大,最大利润为:![]() 元.
元.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目