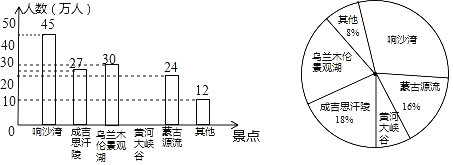
��Ŀ����
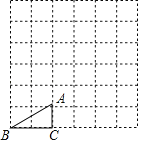
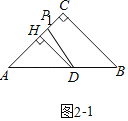
����Ŀ����֪����ABC�У�AC��BC��m��D��AB���ϵ�һ�㣬����B���Ź���D��ֱ���۵���ʹ��B����AC�ߵĵ�P���������A��C�غϣ����ۺ۽�BC���ڵ�E��
��1��������֪ ��ͼ1������C��60����D��AB���е㣬��֤��AP��![]() AC��
AC��
��2����ʽ���� ��ͼ2������C��90����m��6![]() ��AD��7������D��DH��AC�ڵ�H����DH��AP�ij���
��AD��7������D��DH��AC�ڵ�H����DH��AP�ij���
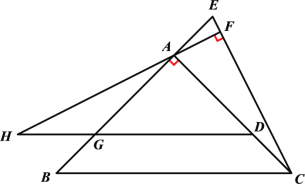
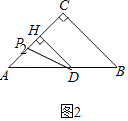
��3������̽�� ��ͼ3����m��10��AB��12���ҵ�AD��aʱ���������β�ͬ���۵���ʹ��B����AC����������ͬ��λ�ã���ֱ��д��a��ȡֵ��Χ��

���𰸡���1��֤������������2��![]() ��4
��4![]() ��3
��3![]() ����3��6��a��
����3��6��a��![]() .
.
��������
��1�����ݵȱ������ε����ʣ����õȱ��������ڽǶ�Ϊ60���Լ�������Ƚ�����⣮
��2���������������ε����ʣ����ö�Ӧ�߳ɱ����Լ����ɶ���������⣮
��3���������Ǻ����Լ����ߺ�һ���ʣ����ù��ɶ����Լ�������ϵ������⣮
��1��֤������AC��BC����C��60����
���ABC�ǵȱ������Σ�
��AC��AB����A��60����
�����⣬��DB��DP��DA��DB��
��DA��DP��
���ADPʹ�õȱ������Σ�
��AP��AD��![]() AB��
AB��![]() AC��
AC��
��2���⣺��AC��BC��6![]() ����C��90����
����C��90����
��AB��![]() ��
��![]() ��12��
��12��
��DH��AC��
��DH��BC��
���ADH�ס�ABC��
��![]() ��
��![]() ��
��
��AD��7��
��![]() ��
��![]() ��
��
��DH��![]() ��
��
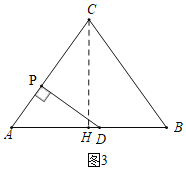
����B�ع���D��ֱ���۵���
����һ������B�����߶�CH�ϵĵ�P1��ʱ����ͼ2��1�У�
��AB��12��
��DP1��DB��AB��AD��5��
��HP1��![]() ��
��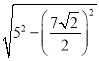 ��
��![]() ��
��
��A1��AH+HP1��4![]() ��
��
���ζ�������B�����߶�AH�ϵĵ�P2��ʱ����ͼ2��2�У�
ͬ����֤HP2��![]() ��
��
��AP2��AH��HP2��3![]() ��
��
��������������������AP��ֵΪ4![]() ��3
��3![]() ��
��
��3����ͼ3�У�����C��CH��AB��H������D��DP��AC��P��
��CA��CB��CH��AB��
��AH��HB��6��
��CH��![]() ��
��![]() ��8��
��8��
��DB��DPʱ����BD��PD��x����AD��12��x��
��tanA��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��x��![]() ��
��
��AD��AB��BD��![]() ��
��
�۲�ͼ�ο�֪��6��a��![]() ʱ���������β�ͬ���۵���ʹ��B����AC����������ͬ��λ�ã�
ʱ���������β�ͬ���۵���ʹ��B����AC����������ͬ��λ�ã�