题目内容
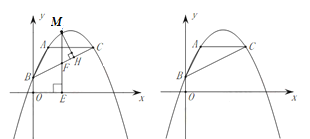
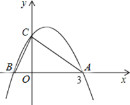
【题目】如图,抛物线![]() 与
与![]() 轴相交于点A(3,0)和
轴相交于点A(3,0)和![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
(1)求![]() 的值和点
的值和点![]() 的坐标;
的坐标;
(2)点D(x,y)是抛物线上一点,若S△ABD= S△ABC,求点![]() 的坐标
的坐标
【答案】(1)m=3,B(1,0);(2)(2,3)或(![]() ,3)或(
,3)或(![]() ,3).
,3).
【解析】
(1)把点A的坐标代入函数解析式,通过解方程来可求m的值,利用抛物线的对称性可求点B的坐标;
(2)设D的坐标为(x,-x2+2x+3),由已知条件易求S△ABC,并且△ABD的高为D的纵坐标的绝对值,进而可建立方程求出x的值即可.
(1)∵抛物线y=x2+2x+m与x轴相交于点A(3,0),
∴32+2×3+m=0,解得:m=3,
∵该抛物线的对称轴为:直线x=1,
∴B(1,0);
(2)∵点D(x,y)是抛物线上一点,
∴设D的坐标为(x,x2+2x+3),
∵AB=4,OC=3,
∴S△ABC=![]() ×4×3=6,
×4×3=6,
∵S△ABD=S△ABC,
∴![]() AB|x2+2x+3|=6,即:x2+2x+3=3或x2+2x+3=-3,
AB|x2+2x+3|=6,即:x2+2x+3=3或x2+2x+3=-3,
∴![]() (舍去),
(舍去),![]() ,
,
∴D的坐标是:(2,3)或(![]() ,3)或(
,3)或(![]() ,3).
,3).

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目