题目内容
【题目】综合与实践
背景阅读:旋转就是将图形上的每一点在平面内绕着旋转中心旋转固定角度的位置移动,其中“旋”是过程,“转”是结果.旋转作为图形变换的一种,具备图形旋转前后对应点到旋转中心的距离相等:对应点与旋转中心所连线段的夹角等于旋转角:旋转前、后的图形是全等图形等性质.所以充分运用这些性质是在解决有关旋转问题的关健.
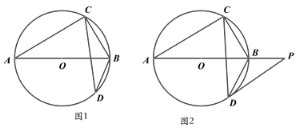
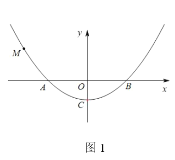
实践操作:如图1,在Rt△ABC中,∠B=90°,BC=2AB=12,点D,E分别是边BC,AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.
问题解决:(1)①当α=0°时,![]() = ;②当α=180°时,
= ;②当α=180°时,![]() = .
= .
(2)试判断:当0°≤a<360°时,![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
问题再探:(3)当△EDC旋转至A,D,E三点共线时,求得线段BD的长为 .
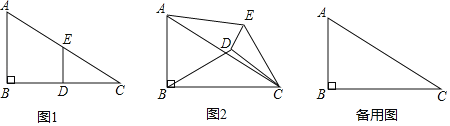
【答案】(1)①![]() ,②
,②![]() ;(2)无变化,证明见解析;(3)6
;(2)无变化,证明见解析;(3)6![]() 或
或![]() .
.
【解析】
问题解决:(1)①根据三角形中位线定理可得:BD=CD![]() BC=6,AE=CE
BC=6,AE=CE![]() AC=3
AC=3![]() ,即可求出
,即可求出![]() 的值;
的值;
②先求出BD,AE的长,即可求出![]() 的值;
的值;
(2)证明△ECA∽△DCB,可得![]() ;
;
问题再探:(3)分两种情况讨论,由矩形的判定和性质以及相似三角形的性质可求BD的长.
问题解决:
(1)①当α=0°时.
∵BC=2AB=12,
∴AB=6,
∴AC![]() 6
6![]() ,
,
∵点D、E分别是边BC、AC的中点,
∴BD=CD![]() BC=6,AE=CE
BC=6,AE=CE![]() AC=3
AC=3![]() ,DE
,DE![]() AB,
AB,
∴![]() .
.
故答案为:![]() ;
;
②如图1.
 ,
,
当α=180°时.
∵将△EDC绕点C按顺时针方向旋转,
∴CD=6,CE=3![]() ,
,
∴AE=AC+CE=9![]() ,BD=BC+CD=18,
,BD=BC+CD=18,
∴![]() .
.
故答案为:![]() .
.
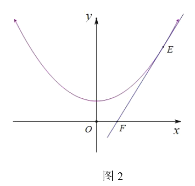
(2)如图2,
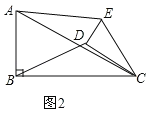 ,
,
当0°≤α<360°时,![]() 的大小没有变化.证明如下:
的大小没有变化.证明如下:
∵∠ECD=∠ACB,
∴∠ECA=∠DCB,
又∵![]() ,
,
∴△ECA∽△DCB,
∴![]() .
.
问题再探:
(3)分两种情况讨论:
①如图3.
 .
.
∵AC=6![]() ,CD=6,CD⊥AD,
,CD=6,CD⊥AD,
∴AD![]() 12.
12.
∵AD=BC,AB=DC,
∴四边形ABCD是平行四边形.
∵∠B=90°,
∴四边形ABCD是矩形,
∴BD=AC=6![]()
②如图4,连接BD,过点D作AC的垂线交AC于点Q,过点B作AC的垂线交AC于点P.
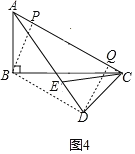
∵AC=6![]() ,CD=6,CD⊥AD,
,CD=6,CD⊥AD,
∴AD![]() 12.
12.
在Rt△CDE中,DE=![]() =3,
=3,
∴AE=AD﹣DE=12﹣3=9,
由(2)可得:![]() ,
,
∴BD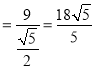 .
.
综上所述:BD=6![]() 或
或![]() .
.
故答案为:6![]() 或
或![]() .
.

【题目】如今很多初中生喜欢购头饮品饮用,既影响身体健康又给家庭增加不必要的开销,为此某班数学兴趣小组对本班同学一天饮用饮品的情况进行了调查,大致可分为四种:A.白开水,B.瓶装矿泉水,C.碳酸饮料,D.非碳酸饮料.根据统计结果绘制如下两个统计图,根据统计图提供的信息,解答下列问题
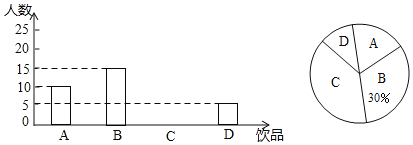
(1)这个班级有多少名同学?并补全条形统计图;
(2)若该班同学每人每天只饮用一种饮品(每种仅限一瓶,价格如下表),则该班同学每天用于饮品的人均花费是多少元?
饮品名称 | 白开水 | 瓶装矿泉水 | 碳酸饮料 | 非碳酸饮料 |
平均价格(元/瓶) | 0 | 2 | 3 | 4 |
(3)为了养成良好的生活习惯,班主任决定在饮用白开水的5名班委干部(其中有两位班长记为A,B,其余三位记为C,D,E)中随机抽取2名班委干部作良好习惯监督员,请用列表法或画树状图的方法求出恰好抽到2名班长的概率.