Question

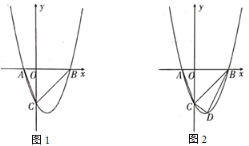
【题目】如图，在平面直角坐标系中，抛物线，经过点、，过点作轴的平行线交抛物线于另一点．

(1)求抛物线的表达式及其顶点坐标；

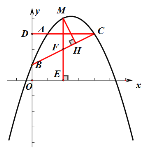
(2)如图，点是第一象限中上方抛物线上的一个动点，过点作于点，作轴于点，交于点，在点运动的过程中，的周长是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由；

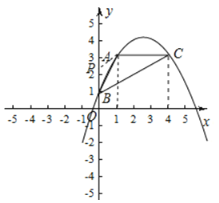
(3)如图，连接，在轴上取一点，使和相似，请求出符合要求的点坐标．

Answer 1

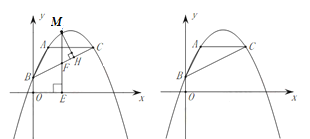
【答案】（1）抛物线的解析式为，顶点坐标为；（2）最大值为；（3）满足条件的点有，．

【解析】

（1）将A（1，3），B（0，1），代入抛物线y=x2+bx+c，即可得出答案；

（2）延长CA交y轴于点D，由点C（4，3）可求得＝，由tan∠C=tan∠M＝＝，设M（a，a2+a+1），求得F(a，a+1)，则MF=a2+2a，由勾股定理得，FH＝MF，MH＝MF，所以△MFH的周长可用MF表示，最后利用二次函数的性质解决问题；

（3）由＝，∠CDB为公共角，可得△ABD∽△BCD．从而∠ABD=∠BCD．分1°当∠PAB=∠ABC时，2°当∠PAB=∠BAC时两种情况讨论即可得出答案．

（1）将，，代入，

解得，．

抛物线的解析式为．

顶点坐标为．

（2）由，得直线解析式为：

设M，则得

则

∵

∴有最大值，当时，最大值为2

将直线与轴交点记作，

易得

因为轴，∴

又∵，∴∽

∴

∴

所以的最大值为

（3） ，为公共角，

．

．

当时，，

，

，

，

．

当时，，

，

，

．

综上所述满足条件的点有，．