题目内容
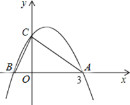
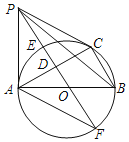
【题目】如图,⊙O是△ABC的外接圆,AB是直径,OD⊥AC,垂足为D点,直线OD与⊙O相交于E,F两点,P是⊙O外一点,P在直线OD上,连接PA,PB,PC,且满足∠PCA=∠ABC
(1)求证:PA=PC;
(2)求证:PA是⊙O的切线;
(3)若BC=8,![]() ,求DE的长.
,求DE的长.
【答案】(1)详见解析;(2)详见解析;(3)DE=8.
【解析】
(1)根据垂径定理可得AD=CD,得PD是AC的垂直平分线,可判断出PA=PC;
(2)由PC=PA得出∠PAC=∠PCA,再判断出∠ACB=90°,得出∠CAB+∠CBA=90°,再判断出∠PCA+∠CAB=90°,得出∠CAB+∠PAC=90°,即可得出结论;
(2)根据AB和DF的比设AB=3a,DF=2a,先根据三角形中位线可得OD=4,从而得结论.
(1)证明∵OD⊥AC,
∴AD=CD,
∴PD是AC的垂直平分线,
∴PA=PC,
(2)证明:由(1)知:PA=PC,
∴∠PAC=∠PCA.
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠CAB+∠CBA=90°.
又∵∠PCA=∠ABC,
∴∠PCA+∠CAB=90°,
∴∠CAB+∠PAC=90°,即AB⊥PA,
∴PA是⊙O的切线;
(3)解:∵AD=CD,OA=OB,
∴OD∥BC,OD=![]() BC=
BC=![]() =4,
=4,
∵![]() ,
,
设AB=3a,DF=2a,
∵AB=EF,
∴DE=3a﹣2a=a,
∴OD=4=![]() ﹣a,
﹣a,
a=8,
∴DE=8.

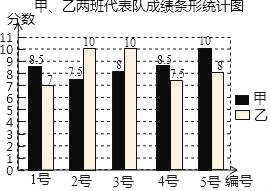
【题目】甲、乙两班分别选5名同学组成代表队参加学校组织的“国防知识”选拔赛,现根据成绩(满分10分)制作如图统计图和统计表(尚未完成)
甲、乙两班代表队成绩统计表
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | 8.5 | a | 0.7 |
乙班 | 8.5 | b | 10 | 1.6 |
请根据有关信息解决下列问题:
(1)填空:a= ,b= ;
(2)学校预估如果平均分能达8.5分,在参加市团体比赛中即可以获奖,现应选派 代表队参加市比赛;(填“甲”或“乙”)
(3)现将从成绩满分的3个学生中随机抽取2人参加市国防知识个人竞赛,请用树状图或列表法求出恰好抽到甲,乙班各一个学生的概率.