Question

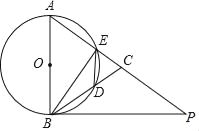
【题目】如图，在△ABC中，∠ABC=2∠C，AP和BQ分别为∠BAC和∠ABC的角平分线，若△ABQ的周长为18，BP=4，则AB的长为_____________

Answer 1

【答案】7

【解析】

根据角平分线的定义得到∠CBQ=∠ABC，再由等角对等边得到CQ=BQ，得到BQ+AQ=CQ+AQ=AC；过点P作PD∥BQ，由“AAS”可证△ABP≌△ADP，由全等三角形的性质可得AB=AD，BP=DP，得到AB+BP=AD+CD=AC，即BQ+AQ=AB+BP，即可得出AB的长．

解：∵BQ是∠ABC的角平分线，

∴∠CBQ=∠ABC．

又∵∠ABC=2∠C，

∴∠CBQ=∠ABC=∠C，

∴ BQ=CQ，

∴ BQ+AQ=CQ+AQ=AC（1）．

如图所示，过点P作PD∥BQ交CQ于点D，

则∠CPD=∠CBQ，∠ADP=∠AQB，

∵∠AQB=∠C+∠CBQ=2∠C，

∴∠ADP=2∠C，

∴∠ABC=∠ADP．

又∵AP是∠BAC的角平分线，

∴∠BAP=∠CAP．

在△ABP和△ADP中，

，

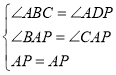∴△ABP≌△ADP（AAS），

∴AB=AD，BP=DP，

∴AB+BP=AD+CD=AC（2），

由（1）（2）得：BQ+AQ=AB+BP，

又∵△ABQ的周长为18，BP=4，

∴18－AB= AB+4，

∴ AB=7．

故答案为：7．