题目内容
【题目】已知一次函数y=2x+4,

(1)在如图所示的平面直角坐标系中,画出函数的图象.
(2)求图象与x轴的交点A的坐标,与y轴交点B的坐标.
(3)利用图象直接写出:当y<0时,x的取值范围.
【答案】(1)画图见解析;(2)A(-2,0),B(0,4);(3)x<-2.
【解析】
(1)利用两点法就可以画出函数图象;(2)利用函数解析式分别代入x=0与y=0的情况就可以求出交点坐标;(3)观察函数图象与x轴的交点,找出在x轴下方的图象即可得出结论.
(1)∵当x=0时,y=4,当y=0时x=-2,
∴函数的图象如图所示:
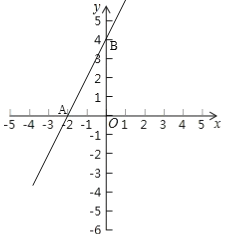
(2)由(1)可知A(-2,0),B(0,4).
(3)由图象可知一次函数图象在x轴下方时,x<-2,
∴y<0时,x的取值范围是x<-2.

【题目】浠水县商场某柜台销售每台进价分别为160元、120元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 4台 | 1200元 |
第二周 | 5台 | 6台 | 1900元 |
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,商场销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
【题目】九年级(3)班数学兴趣小组经过市场调查,整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
时间x(天) | 1 | 30 | 60 | 90 |
每天的销 售量p(件) | 198 | 140 | 80 | 20 |
(1)求出w与x之间的函数表达式;
(2)销售该商品在第几天时,当天获得的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.






