Question

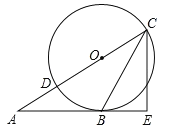
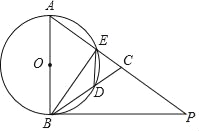
【题目】在△ABC中，AB＝AC，以AB为直径的⊙O交AC于点E，交BC于点D，P为AC延长线上一点，且∠PBC＝∠BAC，连接DE，BE．

（1）求证：BP是⊙O的切线；

（2）若sin∠PBC＝，AB＝10，求BP的长．

Answer 1

【答案】（1）证明见解析；（2）

【解析】

（1）连接AD，求出∠PBC＝∠ABC，求出∠ABP＝90°，根据切线的判定得出即可；

（2）解直角三角形求出BD，求出BC，根据勾股定理求出AD，根据相似三角形的判定和性质求出BE，根据相似三角形的性质和判定求出BP即可．

（1）连接AD，

∵AB是⊙O的直径，

∴∠ADB=90°，

∴AD⊥BC，

∵AB=AC，

∴AD平分∠BAC，

∴∠BAD=∠BAC，

∵∠ADB=90°，

∴∠BAD+∠ABD=90°，

∵∠PBC=∠BAC，

∴∠PBC+∠ABD=90°，

∴∠ABP=90°，即AB⊥BP，

∴PB是⊙O的切线；

（2）∵∠PBC=∠BAD，

∴sin∠PBC=sin∠BAD，

∵sin∠PBC==，AB=10，

∴BD=2，由勾股定理得：AD==4，

∴BC=2BD=4，

∵由三角形面积公式得：AD×BC=BE×AC，

∴4×4=BE×10，

∴BE=8，

∴在Rt△ABE中，由勾股定理得：AE=6，

∵∠BAE=∠BAP，∠AEB=∠ABP=90°，

∴△ABE∽△APB，

∴=，

∴PB===．