题目内容
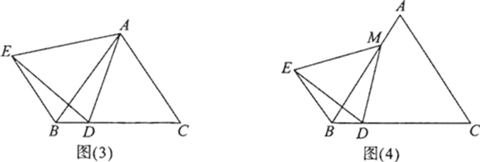
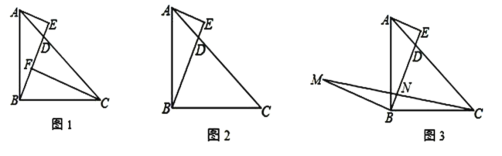
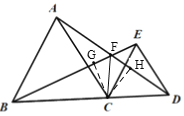
【题目】已知,如图△ABC和△CDE均为等边三角形,B、C、D三点在同一条直线上,连接线段BE、AD交于点F,连接CF,

(1)求证:∠FBC=∠FAC.
(2)求∠BFC的度数.
【答案】(1)证明见解析;(2)∠BFC=60°.
【解析】
(1)根据等边三角形的性质可得∠ECD=∠ABC=60°,AC=BC,CD=CE,利用角的和差关系可得∠ACD=∠BCE,利用SAS可证明△ACD≌△BCE,根据全等三角形的性质即可得答案;(2)作CG⊥BE于G,CH⊥AD于H,由∠ACB=∠EDC=60°可得AC//ED,根据平行线的性质可得∠CAD=∠ADE,利用等量代换可得∠EBD=∠ADE,根据三角形外角性质可得∠EFD=∠EBD+∠BDF=∠ADE+∠BDF=∠BDE=60°,根据平角的定义可得∠BFD=120°,由(1)得△ACD≌△BCE,根据全等三角形对应边上的高对应相等可得CG=CH,根据角平分线的性质可得CF是∠BFD的角平分线,即可求出∠BFC的度数.
(1)∵△ABC和△CDE均为等边三角形,
∴AC=BC,∠ACB=∠ECD=60°,CD=CE,
∴∠ACB+∠ACE=∠ECD+∠ACE,即∠ACD=∠BCE,
在△ACD和△BCE中, ,
,
∴△ACD≌△BCE,
∴∠EBC=∠DAC,即∠FBC=∠FAC.
(2)∵∠ACB=∠EDC=60°,
∴AC//DE,
∴∠CAD=∠ADE,
∵∠CAD=∠EBD,
∴∠EBD=∠ADE,
∴∠EFD=∠EBD+∠BDF=∠ADE+∠BDF=∠EDB=60°,
∴∠BFD=180°-∠EFD=120°,
∵△ACD≌△BCE,CG、CH分别是对应边BE、AD的高,
∴CG=CH,
∴CF是∠BFD的角平分线,
∴∠BFC=![]() ∠BFD=60°.
∠BFD=60°.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】(7分)某中学1000名学生参加了”环保知识竞赛“,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)作为样本进行统计,并制作了如图频数分布表和频数分布直方图(不完整且局部污损,其中“■”表示被污损的数据).请解答下列问题:
成绩分组 | 频数 | 频率 |
50≤x<60 | 8 | 0.16 |
60≤x<70 | 12 | a |
70≤x<80 | ■ | 0.5 |
80≤x<90 | 3 | 0.06 |
90≤x≤100 | b | c |
合计 | ■ | 1 |
(1)写出a,b,c的值;
(2)请估计这1000名学生中有多少人的竞赛成绩不低于70分;
(3)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取两名同学参加环保知识宣传活动,求所抽取的2名同学来自同一组的概率.