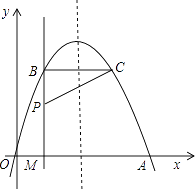题目内容
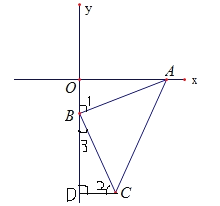
【题目】如图,已知A(3,0),B(0,-1),连接AB,过B点作AB的垂线段,使BA=BC,连接AC.
(1)如图1,求C点坐标;
(2)如图2,若P点从A点出发,沿x轴向左平移,连接BP,作等腰直角三角形△BPQ,连接CQ.求证:PA=CQ.
(3)在(2)的条件下,若C、P、Q三点共线,求此时P点坐标及∠APB的度数.

【答案】(1)C(1,-4).(2)证明见解析;(3)∠APB=135°,P(1,0).
【解析】试题分析:(1)过C作CD⊥Y轴于D,证出△ABO≌△BCD,再由OB=DC,OA=DB得出C(1,-4);
(2)证出△APB≌△CQB,进而得出PA=CQ;
(3)由C、P、Q三点共线,得∠CQB=135°,即∠APB=135°,进而∠OPB=45°,得P(1,0).
试题解析:(1)过C作CD⊥Y轴于D,
∴∠AOB=∠BDC=90°, ∠2+∠3=90°,
∵BC⊥AB,
∴∠1+∠3=90°,
∴∠1=∠2,
在△ABO和△BCD中, 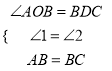 ,
,
∴△ABO≌△BCD,
∴OB=DC, OA=DB
∴C(1,-4);
(2)∵∠ABQ+∠QBC=∠PBA+∠ABQ=90°,
∴∠QBC=∠PBA,
在△APB和△CQB中, 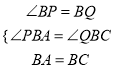 ,
,
∴△APB≌△CQB,(AAS)
∴AP=CQ;
(2)∵△APB≌△CQB,
∴∠APB=∠CQB,
∵由C、P、Q三点共线,
∴∠CQB=135°,即∠APB=135°,
∴∠OPB=45°,
∴P(1,0).

【题目】某电器超市销售每台进价分别为2000元、1700元的A、B两种型号的空调,如表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
(进价、售价均保持不变,利润=销售总收入进货成本)
(1)求A、B两种型号的空调的销售单价;
(2)若超市准备用不多于54000元的金额再采购这两种型号的空调共30台,求A种型号的空调最多能采购多少台?