题目内容
【题目】[材料阅读]
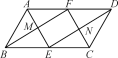
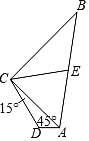
材料一:如图,![]() ,点
,点![]() 在
在![]() 的平分线
的平分线![]() 上,
上,![]() ,点
,点![]() ,D分别在
,D分别在![]() 上.可求得如下结论:
上.可求得如下结论:![]() ,
,![]() 为定值.
为定值.
材料二(性质):四边形的内角和为![]() .
.
[问题解决]
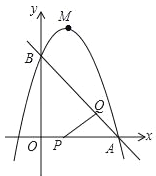
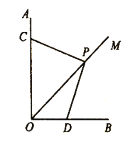
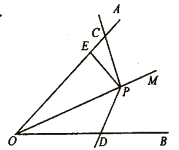
(1)如图,点![]() 在
在![]() 的平分线
的平分线![]() 上,
上,![]() 的边与
的边与![]() 交于点
交于点![]() ,且
,且![]() ,求
,求![]() 的值(用含
的值(用含![]() 的式子表示).
的式子表示).
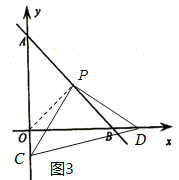
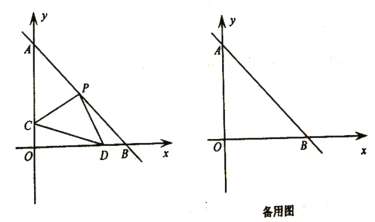
(2)如图,在平面直角坐标系中,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 两点,点
两点,点![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 与
与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,连接
,连接![]() .求
.求![]() 的长度.
的长度.
【答案】(1)![]() ;(2)
;(2)![]() 的长度为
的长度为![]() 或
或![]()
【解析】
(1)如图1,作![]() 于点F,根据角平分线的性质可得PE=PF,再根据材料二的结论和已知条件可得∠OCP=∠FDP,进一步即可根据AAS证明
于点F,根据角平分线的性质可得PE=PF,再根据材料二的结论和已知条件可得∠OCP=∠FDP,进一步即可根据AAS证明![]() ,从而得
,从而得![]() ,由勾股定理易得
,由勾股定理易得![]() ,进而可推出
,进而可推出![]() ,而OE可根据勾股定理求出,于是可得结论;
,而OE可根据勾股定理求出,于是可得结论;
(2)分情况讨论:①若点C在线段AO上,由一次函数与坐标轴的交点可得OA=OB=7,可得△AOB是等腰直角三角形,如图2,连接![]() ,根据等腰直角三角形的性质和余角的性质可得OP=BP,∠PBO=∠POA =45°,∠OPC=∠BPD,进而可根据ASA证明
,根据等腰直角三角形的性质和余角的性质可得OP=BP,∠PBO=∠POA =45°,∠OPC=∠BPD,进而可根据ASA证明![]() ,可得
,可得![]() ,然后在
,然后在![]() 中利用勾股定理即可求出CD;
中利用勾股定理即可求出CD;
②若点C在射线AO上,如图3,连接![]() ,仿①的思路利用ASA证明
,仿①的思路利用ASA证明![]() ,可得
,可得![]() ,然后在
,然后在![]() 中利用勾股定理求解即可.
中利用勾股定理求解即可.
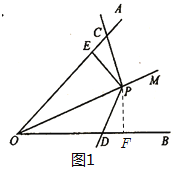
解:(1)如图1,作![]() 于点F,∵PO平分∠AOB,PE⊥OA,∴PE=PF,
于点F,∵PO平分∠AOB,PE⊥OA,∴PE=PF,
在四边形OCPD中,∵![]() ,∴由材料二的结论得:
,∴由材料二的结论得:![]() ,
,
∵![]() ,∴∠OCP=∠FDP,
,∴∠OCP=∠FDP,
在△PEC和△PFD中,∵∠OCP=∠FDP,∠CEP=∠DFP=90°,PE=PF,
∴![]() (AAS),∴
(AAS),∴![]() .
.
∵![]() ,PE=PF,∴
,PE=PF,∴![]() .
.
∴![]() ,
,
在![]() 中,∵
中,∵![]() ,∴
,∴![]() ;
;
(2)分情况讨论:①若点C在线段AO上,由直线![]() ,可得
,可得![]() ,A(0,7),∴OA=OB=7,∴△AOB是等腰直角三角形,
,A(0,7),∴OA=OB=7,∴△AOB是等腰直角三角形,
如图2,连接![]() ,∵P为AB中点,∴OP=AP=BP,∠PBO=∠POC=∠POB=45°,∠OPB=90°,
,∵P为AB中点,∴OP=AP=BP,∠PBO=∠POC=∠POB=45°,∠OPB=90°,
∵![]() ,∴∠BPD+∠OPD=90°,
,∴∠BPD+∠OPD=90°,
∵∠OPC+∠OPD=90°,∴∠OPC=∠BPD,
∴![]() (ASA),∴
(ASA),∴![]() ,
,
又∵OB=7,∴OD=5,则在![]() 中,
中,![]() ;
;
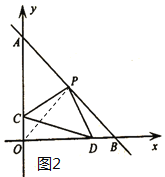
②若点C在射线AO上,如图3,连接![]() ,
,
∵△AOB是等腰直角三角形,P为AB中点,
∴OP=BP,∠PBO=∠POA =45°,∠OPB=90°,
∴∠POC=∠PBD=135°,
又∵![]() ,∴∠BPD+∠CPB=90°,
,∴∠BPD+∠CPB=90°,
∵∠OPC+∠CPB=90°,∴∠OPC=∠BPD,
∴![]() (ASA),∴
(ASA),∴![]() ,
,
∵OB=7,∴![]() ,则在
,则在![]() 中,
中,![]() .
.
综上所述,![]() 的长度为
的长度为![]() 或
或![]() .
.