题目内容
【题目】如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，∠ACD=3∠BCD，E是斜边AB的中点,则∠ECD的度数为__________度.
【答案】45°
【解析】
求出∠ACD=67.5°，∠BCD=22.5°，根据三角形内角和定理求出∠B=67.5°，根据直角三角形斜边上中线性质求出BE=CE，推出∠BCE=∠B=67.5°，代入∠ECD=∠BCE-∠BCD求出即可．
∵∠ACD=3∠BCD,∠ACB=90°，
∴∠ACD=67.5°,∠BCD=22.5°，
∵CD⊥AB，
∴∠CDB=90°，
∴∠B=180°90°22.5°=67.5°，
∵∠ACB=90°，E是斜边AB的中点，
∴BE=CE，
∴∠BCE=∠B=67.5°，
∴∠ECD=∠BCE∠BCD=67.5°22.5°=45°.
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
【题目】中华文明，源远流长，中华汉字，寓意深广。为了传承优秀传统文化，某校团委组织了一次全校1500名学生参加的“汉字听写”大赛，为了更好地了解本次大赛的成绩分布情况，随机抽取了部分学生的成绩作为样本进行整理，得到下列不完整的统计图表． 请你根据表中提供的信息，解答下列问题：
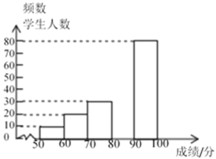
成绩x/分 | 频数 | 频率 |
50≤x＜60 | 10 | 0.05 |
60≤x＜70 | 20 | 0.10 |
70≤x＜80 | 30 | b |
80≤x＜90 | a | 0.30 |
90≤x≤100 | 80 | 0.40 |
（1）此次调查的样本容量为_____；
（2）在表中：
=_____，
=______；
（3）补全频数分布直方图；
（4）若成绩在80分以上（包括80分）的为“A”级，则该校参加这次比赛的1500名学生中，成绩为“A”级的约有多少人？
