题目内容
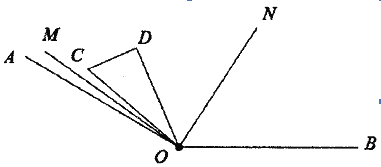
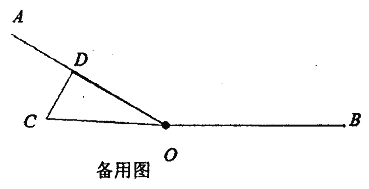
【题目】如图，已知
，将一个直角三角形纸片(
)的一个顶点放在点
处，现将三角形纸片绕点任意转动，
平分斜边
与
的夹角，
平分
.
（1）将三角形纸片绕点转动(三角形纸片始终保持在
的内部)，若
，则
_______；
（2）将三角形纸片绕点转动(三角形纸片始终保持在的内部)，若射线
恰好平方
，若
，求
的度数;
（3）将三角形纸片绕点从与重合位置逆时针转到与重合的位置，猜想在转动过程中和的数量关系？并说明理由.
【答案】（1）
；（2）
；（3）
，证明见解析
【解析】
（1）利用角平分线定义得出
，
，再利用∠AOB的和差关系进行列方程即可求解；
（2）利用
，表达出∠AOC、∠BOD，利用∠AOB的和差关系进行列方程即可求解；
（3）画出图形后利用角的和差关系进行计算求解即可．
解：（1）∵
平分斜边
与
的夹角，
平分
．
∴OM平分∠AOC, ON平分∠BOD
∴设
∴
，
∵
∴
∴
故答案为:
（2）∵
∴设
∵射线
恰好平方
∴
∴
∵平分斜边与的夹角，平分．
∴OM平分∠AOC, ON平分∠BOD
∴
∴
∵
∴
∴
(3) 
,证明如下：
当OC与OA重合时，设∠COD=x,则
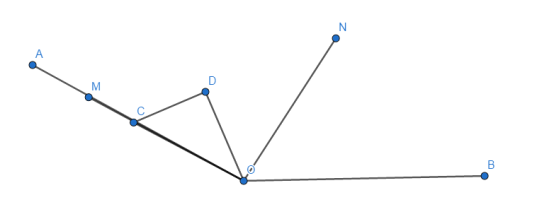
∵ON平分∠BOD
∴
∴
∴
当OC在OA的左侧时
设∠AOD=a，∠AOC=b，则∠BOD=∠AOB-∠AOD=150°-a，∠COD=∠AOD+∠AOC=a+b
∵ON平分∠BOD
∴
∵OM平分∠AOC
∴
∴∠MON=∠MOA+∠AOD+∠DON
当OD与OA重合时
∵ON平分∠AOB
∴
∵OM平分∠AOC
∴
∴
综上所述
练习册系列答案
相关题目
