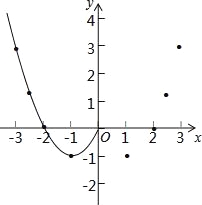题目内容
【题目】如图1，
，
，
是郑州市二七区三个垃圾存放点，点，分别位于点的正北和正东方向，
米，八位环卫工人分别测得的
长度如下表：
甲 | 乙 | 丙 | 丁 | 戊 | 戌 | 申 | 辰 | |
BC（单位：米） | 84 | 76 | 78 | 82 | 70 | 84 | 86 | 80 |
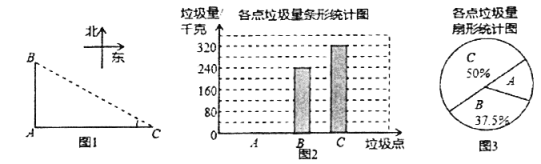
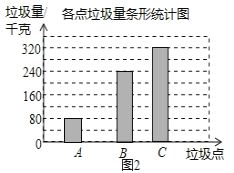
他们又调查了各点的垃圾量，并绘制了下列尚不完整的统计图2，图3：
（1）求表中长度的平均数
、中位数、众数；
（2）求
处的垃圾量，并将图2补充完整；
【答案】（1）
米，
米，
米；（2）
，图见解析.
【解析】
（1）利用平均数等概念求法可得出答案；
（2）利用扇形统计图以及条形统计图可得出
处垃圾量以及所占百分比，进而求出垃圾总量，进而得出
处垃圾量.
（1）
（米），
中位数是：米，众数是：米；
（2）
处垃圾存放量为：
，在扇形统计图中所占比例为：
，
垃圾总量为：
（千克），
处垃圾存放量为：
，占
.
补全条形图如下：
练习册系列答案
相关题目
【题目】某商家计划从厂家采购空调和冰箱两种产品共
台，空调和冰箱的采购单价与销售单价如表所示：
采购单价 | 销售单价 | |
空调 |
|
|
冰箱 |
|
|
若采购空调
台，且所采购的空调和冰箱全部售完，求商家的利润；
厂家有规定，采购空调的数量不少于
台，且空调采购单价不低于
元，问商家采购空调多少台时总利润最大？并求最大利润．
【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究，探究过程如下，请补充完整．
（1）自变量x的取值范围是全体实数，x与y的几组对应值列表：
x | … | ﹣3 | － | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| m | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
其中m= ．
（2）根据上表数据，在如图所示的平面直角坐标系中描点，并画出了函数图象的一部分，请画出该函数图象的另一部分；
（3）观察函数图象，写出2条函数的性质；
（4）进一步探究函数图象发现：
①函数图象与x轴有 个交点，所对应的方程x2﹣2|x|=0有
②方程x2﹣2|x|=2有 个实数根．
