题目内容
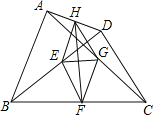
【题目】如图，在等腰三角形
中，
，
，
是
边的中点，点
在线段
上从
向
运动，同时点
在线段
上从点向
运动，速度都是1个单位/秒，时间是
（
），连接
、
、
.
（1）请判断
形状，并证明你的结论.
（2）以、、、四点组成的四边形面积是否发生变化？若不变，求出这个值：若变化，用含的式子表示.
【答案】（1）
为等腰直角三角形，见解析；（2）不变，9
【解析】
⑴连结AD,由SAS定理可证
和
全等，从而可证
,DF=DE.所以为等腰直角三角形.
⑵由割补法可知四边形AEDF的面积不变，利用三角形的面积公式求出答案.
（1）为等腰直角三角形，理由如下：
连接
，
∵
，
，
为
中点
∴
且平分
∴
∵点
、
速度都是1个单位秒，时间是
秒，
∴
在和中，
，
∴
∴
，
∵
∴
即：
∴为等腰直角三角形.
（2）四边形
面积不变，
理由：∵由（1）可知，
，
∴
，
∴
∵
∴
练习册系列答案
相关题目
【题目】如图1，
，
，
是郑州市二七区三个垃圾存放点，点，分别位于点的正北和正东方向，
米，八位环卫工人分别测得的
长度如下表：
甲 | 乙 | 丙 | 丁 | 戊 | 戌 | 申 | 辰 | |
BC（单位：米） | 84 | 76 | 78 | 82 | 70 | 84 | 86 | 80 |
他们又调查了各点的垃圾量，并绘制了下列尚不完整的统计图2，图3：
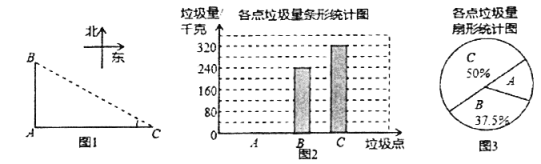
（1）求表中长度的平均数
、中位数、众数；
（2）求
处的垃圾量，并将图2补充完整；
