МвДїДЪИЭ
ЎѕМвДїЎїДіЙМіЎКФПъТ»ЦЦіЙ±ѕОЄГїјю60ФЄµД·юЧ°Ј¬№ж¶ЁКФПъЖЪјдПъКЫµҐјЫІ»µНУЪіЙ±ѕµҐјЫЈ¬ЗТ»сАыІ»µГёЯУЪ45%Ј¬ѕКФПъ·ўПЦЈ¬ПъКЫБї![]() ЈЁјюЈ©УлПъКЫµҐјЫ
ЈЁјюЈ©УлПъКЫµҐјЫ![]() ЈЁФЄЈ©·ыєПТ»ґОєЇКэ
ЈЁФЄЈ©·ыєПТ»ґОєЇКэ![]() Ј¬ЗТ
Ј¬ЗТ![]() К±Ј¬
К±Ј¬![]() Ј»
Ј»![]() К±Ј¬
К±Ј¬![]() Ј®
Ј®
ЈЁ1Ј©ЗуТ»ґОєЇКэ![]() µД±нґпКЅЈ»
µД±нґпКЅЈ»
ЈЁ2Ј©ИфёГЙМіЎ»сµГАыИуОЄ![]() ФЄЈ¬КФРґіцАыИу
ФЄЈ¬КФРґіцАыИу![]() УлПъКЫµҐјЫ
УлПъКЫµҐјЫ![]() Ц®јдµД№ШПµКЅЈ»ПъКЫµҐјЫ¶ЁОЄ¶аЙЩФЄК±Ј¬ЙМіЎїЙ»сµГЧоґуАыИуЈ¬ЧоґуАыИуКЗ¶аЙЩФЄЈї
Ц®јдµД№ШПµКЅЈ»ПъКЫµҐјЫ¶ЁОЄ¶аЙЩФЄК±Ј¬ЙМіЎїЙ»сµГЧоґуАыИуЈ¬ЧоґуАыИуКЗ¶аЙЩФЄЈї
ЈЁ3Ј©ИфёГЙМіЎ»сµГАыИуІ»µНУЪ500ФЄЈ¬КФИ·¶ЁПъКЫµҐјЫ![]() µД·¶О§Ј®
µД·¶О§Ј®
Ўѕґр°ёЎїЅвЈєЈЁ1Ј©Т»ґОєЇКэµД±нґпКЅОЄ![]()
ЈЁ2Ј©µ±ПъКЫµҐјЫ¶ЁОЄ87ФЄК±Ј¬ЙМіЎїЙ»сµГЧоґуАыИуЈ¬ЧоґуАыИуКЗ891ФЄ
ЈЁ3Ј©ПъКЫµҐјЫ![]() µД·¶О§КЗ
µД·¶О§КЗ![]() Ј®
Ј®
ЎѕЅвОцЎї
КФМвЈЁ1Ј©БРіц¶юФЄТ»ґО·ЅіМЧйЅвіцkУлbµДЦµїЙЗуіцТ»ґОєЇКэµД±нґпКЅЈ®
ЈЁ2Ј©ТАМвТвЗуіцWУлxµДєЇКэ±нґпКЅїЙНЖіцµ±x=87К±ЙМіЎїЙ»сµГЧоґуАыИуЈ®
ЈЁ3Ј©УЙw=500НЖіцx2©Ѓ180x+7700=0ЅвіцxµДЦµјґїЙЈ®
КФМвЅвОцЈєЈЁ1Ј©ёщѕЭМвТвµГЈє![]() Ј¬ЅвµГk=©Ѓ1Ј¬b=120Ј®ЛщЗуТ»ґОєЇКэµД±нґпКЅОЄ
Ј¬ЅвµГk=©Ѓ1Ј¬b=120Ј®ЛщЗуТ»ґОєЇКэµД±нґпКЅОЄ![]() Ј»
Ј»
ЈЁ2Ј©![]() =
=![]() Ј¬ЎЯЕЧОпПЯµДїЄїЪПтПВЈ¬Ўаµ±xЈј90К±Ј¬WЛжxµДФцґу¶шФцґуЈ¬¶шПъКЫµҐјЫІ»µНУЪіЙ±ѕµҐјЫЈ¬ЗТ»сАыІ»µГёЯУЪ45%Ј¬јґ60ЎЬxЎЬ60ЎБЈЁ1+45%Ј©Ј¬Ўа60ЎЬxЎЬ87Ј¬Ўаµ±x=87К±Ј¬W=
Ј¬ЎЯЕЧОпПЯµДїЄїЪПтПВЈ¬Ўаµ±xЈј90К±Ј¬WЛжxµДФцґу¶шФцґуЈ¬¶шПъКЫµҐјЫІ»µНУЪіЙ±ѕµҐјЫЈ¬ЗТ»сАыІ»µГёЯУЪ45%Ј¬јґ60ЎЬxЎЬ60ЎБЈЁ1+45%Ј©Ј¬Ўа60ЎЬxЎЬ87Ј¬Ўаµ±x=87К±Ј¬W=![]() =891Ј¬Ўаµ±ПъКЫµҐјЫ¶ЁОЄ87ФЄК±Ј¬ЙМіЎїЙ»сµГЧоґуАыИуЈ¬ЧоґуАыИуКЗ891ФЄЈ®
=891Ј¬Ўаµ±ПъКЫµҐјЫ¶ЁОЄ87ФЄК±Ј¬ЙМіЎїЙ»сµГЧоґуАыИуЈ¬ЧоґуАыИуКЗ891ФЄЈ®
ЈЁ3Ј©Бо![]() =500Ј¬Ѕв·ЅіМ
=500Ј¬Ѕв·ЅіМ![]() Ј¬
Ј¬![]() ЅвµГ
ЅвµГ![]() Ј¬
Ј¬![]() Ј¬УЦЎЯ60ЎЬ
Ј¬УЦЎЯ60ЎЬ![]() ЎЬ87 Ј¬ЛщТФµ±
ЎЬ87 Ј¬ЛщТФµ±![]() ЎЭ500К±Ј¬70ЎЬ
ЎЭ500К±Ј¬70ЎЬ![]() ЎЬ87Ј®
ЎЬ87Ј®

 И«УЕµгБ·µҐФЄјЖ»®ПµБРґр°ё
И«УЕµгБ·µҐФЄјЖ»®ПµБРґр°ёЎѕМвДїЎїТСЦЄ![]() КЗ
КЗ![]() µДєЇКэЈ¬ЧФ±дБї
µДєЇКэЈ¬ЧФ±дБї![]() µДИЎЦµ·¶О§ОЄ
µДИЎЦµ·¶О§ОЄ![]() Ј¬ПВ±нКЗ
Ј¬ПВ±нКЗ![]() Ул
Ул![]() µДјёЧй¶ФУ¦Цµ
µДјёЧй¶ФУ¦Цµ
| 0 | 1 | 2 | 3 | 3.5 | 4 | 4.5 | Ў |
| 1 | 2 | 3 | 4 | 3 | 2 | 1 | Ў |
РЎГчёщѕЭС§П°єЇКэµДѕСйЈ¬АыУГЙПКц±нёсЛщ·ґУііцµД![]() Ул
Ул![]() Ц®јдµД±д»Ї№жВЙЈ¬¶ФёГєЇКэµДНјПуУлРФЦКЅшРРБЛМЅѕї.ПВГжКЗРЎГчµДМЅѕї№эіМЈ¬ЗлІ№ідНкХыЈє
Ц®јдµД±д»Ї№жВЙЈ¬¶ФёГєЇКэµДНјПуУлРФЦКЅшРРБЛМЅѕї.ПВГжКЗРЎГчµДМЅѕї№эіМЈ¬ЗлІ№ідНкХыЈє
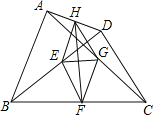
(1)ИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кПµЦРЈ¬ЦёіцБЛТФЙП±нЦРёч¶Ф¶ФУ¦ЦµОЄЧш±кµДµг. ёщѕЭГиіцµДµгЈ¬»іцёГєЇКэµДНјПу.

(2)ёщѕЭ»іцµДєЇКэНјПуМоїХ.
ўЩёГєЇКэНјПуУл![]() ЦбµДЅ»µгЧш±кОЄ_____.
ЦбµДЅ»µгЧш±кОЄ_____.
ўЪЦ±ЅУРґіцёГєЇКэµДТ»МхРФЦК.
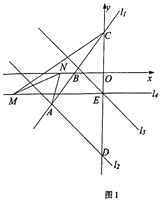
ЎѕМвДїЎїИзНј1Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() КЗЦЈЦЭКР¶юЖЯЗшИэёцА¬»шґж·ЕµгЈ¬µг
КЗЦЈЦЭКР¶юЖЯЗшИэёцА¬»шґж·ЕµгЈ¬µг![]() Ј¬
Ј¬![]() ·Ц±рО»УЪµг
·Ц±рО»УЪµг![]() µДХэ±±єНХэ¶«·ЅПтЈ¬
µДХэ±±єНХэ¶«·ЅПтЈ¬![]() ГЧЈ¬°ЛО»»·ОА№¤ИЛ·Ц±рІвµГµД
ГЧЈ¬°ЛО»»·ОА№¤ИЛ·Ц±рІвµГµД![]() і¤¶ИИзПВ±нЈє
і¤¶ИИзПВ±нЈє
јЧ | ТТ | ±ы | ¶Ў | Ом | Рз | Йк | іЅ | |
BCЈЁµҐО»ЈєГЧЈ© | 84 | 76 | 78 | 82 | 70 | 84 | 86 | 80 |
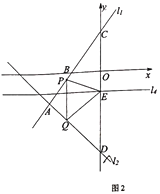
ЛыГЗУЦµчІйБЛёчµгµДА¬»шБїЈ¬Іў»жЦЖБЛПВБРЙРІ»НкХыµДНіјЖНј2Ј¬Нј3Јє
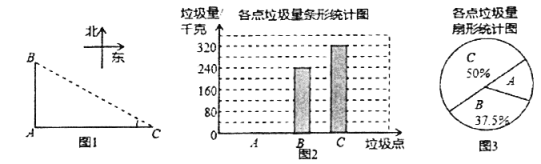
ЈЁ1Ј©Зу±нЦР![]() і¤¶ИµДЖЅѕщКэ
і¤¶ИµДЖЅѕщКэ![]() ЎўЦРО»КэЎўЦЪКэЈ»
ЎўЦРО»КэЎўЦЪКэЈ»
ЈЁ2Ј©Зу![]() ґ¦µДА¬»шБїЈ¬ІўЅ«Нј2І№ідНкХыЈ»
ґ¦µДА¬»шБїЈ¬ІўЅ«Нј2І№ідНкХыЈ»