题目内容
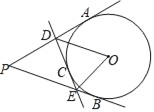
【题目】如图，AD是半圆的直径，点C是弧BD的中点，∠BAD=70°，则∠ADC等于（ ）
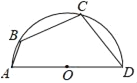
A. 50° B. 55° C. 65° D. 70°
【答案】B
【解析】
连接BD，根据直径所对的圆周角为直角可得∠ABD=90°，即可求得∠ADB=20°，再由圆内接四边形的对角互补可得∠C=110°，因
，即可得BC=DC，根据等腰三角形的性质及三角形的内角和定理可得∠BDC=∠DBC=35°，由此即可得∠ADC=∠ADB+∠BDC=55°．
解：连接BD，
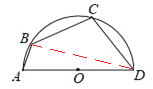
∵AD是半圆O的直径，
∴∠ABD=90°，
∵∠BAD=70°，
∴∠C=110°，∠ADB=20°，
∵ ，
∴BC=DC，
∴∠BDC=∠DBC=35°，
∴∠ADC=∠ADB+∠BDC=55°．
故选B．
练习册系列答案
相关题目
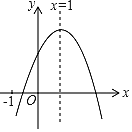
【题目】下表是二次函数
的部分
的对应值：
x | … | －1 |
| 0 |
| 1 |
| 2 |
| 3 | … |
y | … | m |
| －1 |
| －2 |
| －1 |
| 2 | … |
(1)求函数解析式；
(2)当
时，y的取值范围是___________；
(3)当抛物线的顶点在直线
的下方时，n的取值范围是__________.
