题目内容
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示有下列4个结论:①abc>0;②b<a+c;③4a+2b+c>0;④a+b>m(am+b)(m≠1的实数),其中正确结论的个数为( )
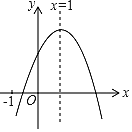
A. 0 B. 1 C. 2 D. 3
【答案】C
【解析】
由抛物线开口向下得到a<0;由抛物线的对称轴为直线x=-![]() =1得到b>0;由抛物线与y轴的交点在x轴的上方得到c>0,则abc<0;观察图象得到当x=-1时,y<0,即a-b+c<0;当x=2时,y>0,即4a+2b+c>0;根据二次函数的最值问题得到x=1时,y有最大值a+b+c,则a+b+c>am2+bm+c(m≠1),变形得到a+b>m(am+b).
=1得到b>0;由抛物线与y轴的交点在x轴的上方得到c>0,则abc<0;观察图象得到当x=-1时,y<0,即a-b+c<0;当x=2时,y>0,即4a+2b+c>0;根据二次函数的最值问题得到x=1时,y有最大值a+b+c,则a+b+c>am2+bm+c(m≠1),变形得到a+b>m(am+b).
∵抛物线开口向下,
∴a<0;
∵抛物线的对称轴为直线x=-![]() =1,
=1,
∴b>0;
∵抛物线与y轴的交点在x轴的上方,
∴c>0,
∴abc<0,故①错误;
当x=-1时,y<0,即a-b+c<0,
∴b>a+c,故②不正确;
当x=2时,y>0,即4a+2b+c>0,故③正确;
∵抛物线的对称轴为直线x=1,
∴x=1时,y有最大值a+b+c,
∴a+b+c>am2+bm+c(m≠1),
∴a+b>m(am+b),故④正确.
故选:C.

【题目】丽水苛公司将“丽水山耕”农副产品运往杭州市场进行销售.记汽车行驶时间为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
v(千米/小时) | 75 | 80 | 85 | 90 | 95 |
t(小时) | 4.00 | 3.75 | 3.53 | 3.33 | 3.16 |
(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从丽水出发,能否在上午10:00之前到达杭州市?请说明理由:
(3)若汽车到达杭州市场的行驶时间t满足3.5≤t≤4,求平均速度v的取值范围.