Question

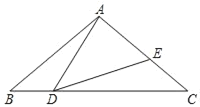
【题目】如图，等腰三角形ABC中，AB＝AC＝4，∠BAC＝100°，点D是底边BC的动点（点D不与B、C重合），连接AD，作∠ADE＝40°，DE与AC交于点E．

（1）当DC等于多少时，△ABD与△DCE全等？请说明理由；

（2）在点D的运动过程中，△ADE的形状可以是等腰三角形吗？若可以，求出∠BDA的度数；若不可以，请说明理由．

Answer 1

【答案】（1）当DC＝4时，△ABD≌△DCE，理由详见解析；（2）当∠BDA的度数为110°或80°时，△ADE的形状是等腰三角形．

【解析】

（1）当DC＝4时，利用∠DEC＋∠EDC＝140，∠ADB＋∠EDC＝140，得到∠ADB＝∠DEC，根据AB＝DC＝4，证明△ABD≌△DCE；

（2）分DA＝DE、AE＝AD、EA＝ED三种情况，根据等腰三角形的性质、三角形内角和定理计算．

解：（1）当DC＝4时，△ABD≌△DCE，

理由：∵AB＝AC＝4，∠BAC＝100，

∴∠B＝∠C＝40，

∴∠DEC+∠EDC＝140，

∵∠ADE＝40，

∴∠ADB+∠EDC＝140，

∴∠ADB＝∠DEC，

在△ABD和△DCE中，

，

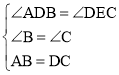∴△ABD≌△DCE（AAS）；

（2）当∠BDA的度数为110或80时，△ADE的形状是等腰三角形，

当DA＝DE时，∠DAE＝∠DEA＝70，

∴∠BDA＝∠DAE+∠C＝70+40＝110；

当AD＝AE时，∠AED＝∠ADE＝40，

∴∠DAE＝100，

此时，点D与点B重合，不合题意；

当EA＝ED时，∠EAD＝∠ADE＝40，

∴∠AED＝100，

∴∠EDC＝∠AED﹣∠C＝60，

∴∠BDA＝180﹣40﹣60＝80

综上所述，当∠BDA的度数为110或80时，△ADE的形状是等腰三角形．