题目内容
【题目】如图，PA、PB、DE切分别切⊙O于点A、B、C，若∠P=50°，则∠DOE=_____°．
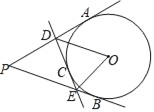
【答案】65
【解析】
连接OA、OC、OB，根据切线的性质定理可得∠DAO=∠EBO=90°，由是必须的内角和为360°可得∠P+∠AOB=180°，由此求得∠AOB=130°，由切线长定理可得∠AOD=∠DOC，∠COE=∠BOE，从而得∠DOE=
∠AOB=65°.
连接OA、OC、OB，
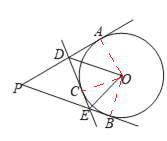
∵OA⊥PA，OB⊥PB，OC⊥DE，
∴∠DAO=∠EBO=90°，
∴∠P+∠AOB=180°，
∴∠AOB=180°﹣50°=130°；
∵∠AOD=∠DOC，∠COE=∠BOE，
∴∠DOE=∠AOB=×130°=65°．
故答案为：65．
练习册系列答案
相关题目
【题目】甲、乙两名队员参加射击训练，成绩分别被制成下列两个统计图：
根据以上信息，整理分析数据如下：
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | c |
（1）写出表格中a，b，c的值；
（2）分别运用表中的四个统计量，简要分析这两名队员的射击训练成绩．若选派其中一名参赛，你认为应选哪名队员．
