题目内容
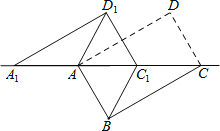
【题目】如图，在△ABD和△ACE中，有下列四个等式：①AB=AC；②AD=AE；③∠1=∠2；④BD=CE．以其中三个条件为题设，填入已知栏中，一个论断为结论，填入下面求证栏中，使之组成一个真命题，并写出证明过程．
已知： ．
求证： ．
证明：
【答案】已知：在△ABD和△ACE中，AB=AC，AD=AE，BD=CE，
求证：∠1=∠2．
【解析】试题分析：此题无论选择什么作为题设，什么作为结论，它有一个相同点﹣﹣都是通过证明△ABD≌△ACE，然后利用全等三角形的性质解决问题．
解：解法一：如果AB=AC，AD=AE，BD=CE，那么∠1=∠2．
已知：在△ABD和△ACE中，AB=AC，AD=AE，BD=CE，
求证：∠1=∠2．
证明：∵AB=AC，AD=AE，BD=CE，
∴△ABD≌△ACE，
∴∠BAD=∠CAE，
∴∠1=∠2．
解法二：如果AB=AC，AD=AE，∠1=∠2，那么BD=CE．
已知：在△ABD和△ACE中，AB=AC，AD=AE，∠1=∠2，
求证：BD=CE．
证明：∵∠1=∠2
∴∠BAD=∠CAE，而AB=AC，AD=AE，
∴△ABD≌△ACE
∴BD=CE．
练习册系列答案
相关题目
【题目】某小组5名同学在一周内参加家务劳动的时间如下表所示，关于“劳动时间”的这组数据，以下说法正确的是（ ）
劳动时间（小时） | 3 | 3.5 | 4 | 4.5 |
人数 | 1 | 1 | 2 | 1 |
A.中位数是4，平均数是3.75
B.众数是4，平均数是3.8
C.众数是2，平均数是3.75
D.众数是2，平均数是3.8
