题目内容
【题目】类比转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.
(1)尝试探究
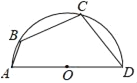
如图(1),在正方形ABCD中,对角线AC、BD相交于点O,点E是BC边上一点,AE与BD交于点G,过点E作EF⊥AE交AC于点F,若![]() =2,则
=2,则![]() 的值是 ;
的值是 ;
(2)拓展迁移
如图(2),在矩形ABCD中,过点B作BH⊥AC于点O,交AD相于点H,点E是BC边上一点,AE与BH相交于点G,过点E作EF⊥AE交AC于点F.
①若∠BAE=∠ACB,sin∠EAF=![]() ,求tan∠ACB;
,求tan∠ACB;
②若![]() ,
,![]() =b(a>0,b>0),求
=b(a>0,b>0),求![]() 的值(用含a,b的代数式表示).
的值(用含a,b的代数式表示).
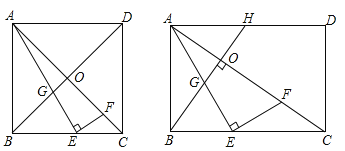
图(1) 图(2)
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]()
【解析】
(1)过E作EN⊥AC于N,EM⊥BD于M,由四边形ABCD是正方形,得到AC⊥BD,∠ACB=∠DBC=45°,于是得到四边形OMEN是矩形,△BEM与△CEN是等腰直角三角形,求得![]() ,然后根据△EMG∽△ENF,即可得到结论;
,然后根据△EMG∽△ENF,即可得到结论;
(2)①过E作EN⊥AC于N,EM⊥BD于M,根据四边形ABCD是矩形,
②过E作EN⊥AC于N,EM⊥BH于M,得到四边形OMEN是矩形,由△MEG∽△NEF,得到![]() 由于△ABC∽△CNE,求出
由于△ABC∽△CNE,求出![]() 由于△BEM∽△BCO,得到
由于△BEM∽△BCO,得到![]() 求出EM=aCN,即可得到结论.
求出EM=aCN,即可得到结论.
(1)过E作EN⊥AC于N,EM⊥BD于M,
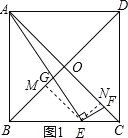
∵四边形ABCD是正方形,
∴AC⊥BD,∠ACB=∠DBC=45°,
∴四边形OMEN是矩形,△BEM与△CEN是等腰直角三角形,
∴![]()
∵![]() =2,∴
=2,∴![]() ,
,
∵EF⊥AE,
∴∠MEG=∠NEF,
∴△EMG∽△ENF,
∴![]()
故答案为:![]() ;
;
(2) ①过E作EN⊥AC于N,EM⊥BD于M,
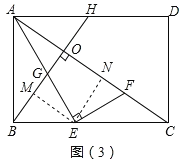
sin∠EAF=![]()
设![]() 则
则![]()
![]()
![]() ∠BAE=∠ACB,
∠BAE=∠ACB,
![]()
![]()
同理可得:![]()
![]()
![]()
点G是AE的中点,
![]()
容易证明![]() ≌
≌![]()
![]()
![]()
![]()
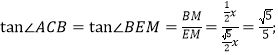
②过E作EN⊥AC于N,EM⊥BH于M,

∵BH⊥AC,
∴四边形OMEN是矩形,
∴![]() ,∵AE⊥EF,
,∵AE⊥EF,
∴∠MEG=∠NEF,
∴△MEG∽△NEF,
∴![]()
∵![]()
∴△ABC∽△CNE,
∴![]()
∴![]()
∵EM⊥BH,AC⊥BH,
∴EM∥AC,
∴△BEM∽△BCO,
∴![]()
∵![]()
∴![]()
∴![]()
∵ON=EM,
∴![]()
∴EM=aCN,
∴![]()
故答案为:![]()

 阅读快车系列答案
阅读快车系列答案