题目内容
【题目】我市规划中某地段地铁线路要穿越护城河PQ,站点A和站点B在河的两侧,要测算出A、B间的距离.工程人员在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q出,测得A位于北偏东49°方向,B位于南偏西41°方向.根据以上数据,求A、B间的距离.(参考数据:cos41°≈0.75)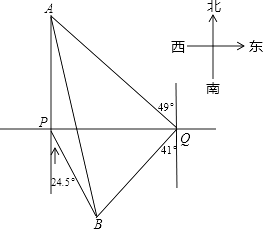
【答案】解:∵∠PQB=90°﹣41°=49°,
∠BPQ=90°﹣24.5°=65.5°,
∴∠PBQ=180°﹣49°﹣65.5°=65.5°,
∴∠BPQ=∠PBQ,
∴BQ=PQ;
∵∠AQB=180°﹣49°﹣41°=90°,∠PQA=90°﹣49°=41°,
∴AQ= ![]() =
= ![]() =1600,
=1600,
∵BQ=PQ=1200,
∴AB2=AQ2+BQ2=16002+12002,
∴AB=2000,
答:A、B的距离为2000m
【解析】首先由已知求出∠PBQ和∠BPQ的度数得出线段BQ与PQ,根据已知求出∠PQA,再由直角三角形PQA求出AQ,又由已知得∠AQB=90°,所以根据勾股定理求出A,B间的距离.
【考点精析】通过灵活运用关于方向角问题,掌握指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角即可以解答此题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目