Question

【题目】已知在四边形ABCD中，∠A=x，∠C=y，（0°＜x＜180°，0°＜y＜180°）．

（1）∠ABC+∠ADC=_____（用含x、y的代数式表示）；

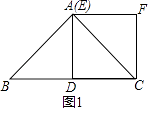
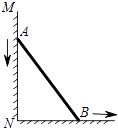
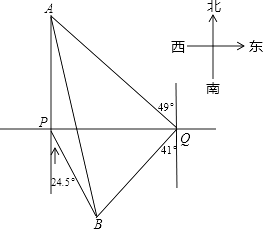
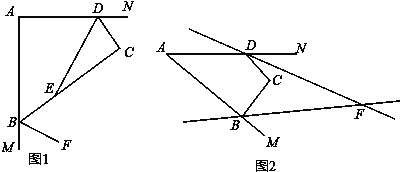
（2）如图1，若x=y=90°，DE平分∠ADC，BF平分与∠ABC相邻的外角，请写出DE与BF的位置关系，并说明理由．

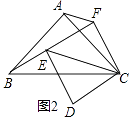
（3）如图2，∠DFB为四边形ABCD的∠ABC、∠ADC相邻的外角平分线所在直线构成的锐角，

①当x＜y时，若x+y=140°，∠DFB=30°试求x、y．

②小明在作图时，发现∠DFB不一定存在，请直接指出x、y满足什么条件时，∠DFB不存在．

Answer 1

【答案】（1）360°-x-y；（2）DE⊥BF，理由见解析；（3）①；②当x、y满足x=y时，∠DFB不存在.

【解析】

（1）利用四边形内角和定理得出答案即可；（2）利用角平分线的性质结合三角形外角的性质得出即可；（3）①利用角平分线的性质以及三角形内角和定理，得出∠DFB=y-x=30°，进而得出x，y的值；②当x=y时，∠ABC、∠ADC相邻的外角平分线所在直线互相平行，此时∠DFB不存在．

（1）∵四边形内角和为（4-2）×180°=360°，

∴∠ABC+∠ADC=360°-x-y，

故答案为：360°-x-y

(2)DE⊥BF，理由如下：

如图：延长DE交BF于G，

∵DE平分∠ADC，BF平分∠MBC，

∴∠CDE=∠ADC，∠CBF=∠CBM，

∵x=y=90°，

∴∠CBM=180°－∠ABC=180°－(180°－∠ADC)=∠ADC，

∴∠CDE=∠CBF，

∵∠BED=∠CDE+∠C=∠CBF+∠BGE，

∴∠BGE=∠C=90°，

∴DG⊥BF，即DE⊥BF

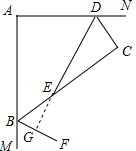
(3)①如图，连接DB，

∵∠A+∠ADC+∠C+∠ABC=360°，∠CDN=180°-∠ADC，∠CBM=180°-∠ABC，

∴∠CDN+∠CBM=∠A+∠C=x+y，

∵BF、DF分别平分∠CBM、∠CDN，

∴∠CDF+∠CBF=(x+y)，

∴∠FBD+∠FDB=180°-y+(x+y)=180°-y+x，

∴∠DFB=180°-(∠FBD+∠FDB)=y-x=30°，

解方程组：，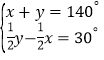

解得：，

∴x=40°，y=100°.

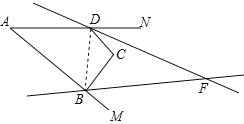
②当x=y时，此时∠DFB=0，即∠ABC、∠ADC相邻的外角平分线所在直线互相平行，故当x、y满足x=y时，∠DFB不存在.