题目内容
【题目】矩形ABCD中,AD=8cm,AB=6cm.动点E从点C开始沿边CB向点B以2cm/s的速度运动,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是下图中的( )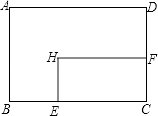
A.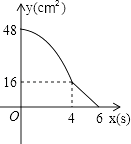
B.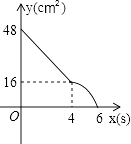
C.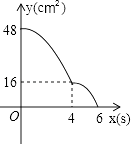
D.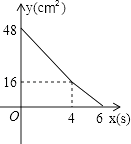
【答案】A
【解析】此题在读懂题意的基础上,分两种情况讨论:
当x≤4时,y=6×8﹣(x2x)=﹣2x2+48,此时函数的图象为抛物线的一部分,它的最上点抛物线的顶点(0,48),最下点为(4,16);
当4<x≤6时,点E停留在B点处,故y=48﹣8x=﹣8x+48,此时函数的图象为直线y=﹣8x+48的一部分,它的最上点可以为(4,16),它的最下点为(6,0).
结合四个选项的图象知选A项.
故答案为:A.
当x≤4时,EC=2x,CF=x,然后依据y两个矩形的面积之差可得到y与x之间的函数关系式,此时函数的图象为抛物线的一部分,它的最上点抛物线的顶点(0,48),最下点为(4,16),CE=CB=8,CF=x,然后再依据y两个矩形的面积之差可得到y与x的函数关系式.

【题目】某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
修造人 | 笔试成绩/分 | 面试成绩/分 |
甲 | 90 | 88 |
乙 | 84 | 92 |
丙 | x | 90 |
丁 | 88 | 86 |
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.