��Ŀ����
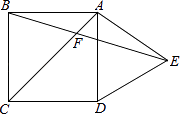
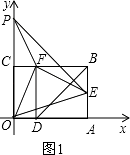
����Ŀ����ͼ���Ծ���OABC�Ķ���OΪԭ�㣬OA���ڵ�ֱ��Ϊx�ᣬOC���ڵ�ֱ��Ϊy�ᣬ����ƽ��ֱ������ϵ����֪OA=3��OC=2����E��AB���е㣬��OA��ȡһ��D������BDA��BD���ۣ�ʹ��A����BC���ϵĵ�F����
��1��ֱ��д����E��F�����ꣻ
��2���趥��ΪF�������߽�y���������ڵ�P�����Ե�E��F��PΪ������������ǵ��������Σ���������ߵĽ���ʽ��
��3����x�ᡢy�����Ƿ�ֱ���ڵ�M��N��ʹ���ı���MNFE���ܳ���С��������ڣ�����ܳ�����Сֵ����������ڣ���˵�����ɣ�
���𰸡�
��1���⣺E��3��1����F��1��2����
��2���⣺��Rt��EBF�У���B=90�㣬
��EF= ![]() ��
��
���P��������0��n��������n��0��
�߶���F��1��2����
���������߽���ʽΪy=a��x��1��2+2��a��0����
�� ��ͼ1��
��EF=PFʱ��EF2=PF2��
��12+��n��2��2=5��
���n1=0����ȥ����n2=4��
��P��0��4����
��4=a��0��1��2+2��
���a=2��
�������ߵĽ���ʽΪy=2��x��1��2+2
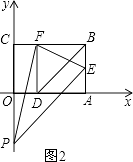
�� ��ͼ2��
��EP=FPʱ��EP2=FP2��
�ࣨ2��n��2+1=��1��n��2+9��
��� ![]() ����ȥ��
����ȥ��
�۵�EF=EPʱ��EP= ![]() ��������������ڣ�
��������������ڣ�
�������������������������߽���ʽ��y=2��x��1��2+2��
��3���⣺���ڵ�M��N��ʹ���ı���MNFE���ܳ���С��
��ͼ3������E����x��ĶԳƵ�E�䣬����F����y��ĶԳƵ�F�䣬 
����E��F�䣬�ֱ���x�ᡢy�ύ�ڵ�M��N�����M��N��������㣮
��E�䣨3����1����F�䣨��1��2����NF=NF�䣬ME=ME�䣮
��BF��=4��BE��=3��
��FN+NM+ME=F��N+NM+ME��=E��F��= ![]() ��
��
�֡� ![]() ��
��
��FN+MN+ME+EF=5+ ![]() ����ʱ�ı���MNFE���ܳ���Сֵ��
����ʱ�ı���MNFE���ܳ���Сֵ�� ![]() ��
��
����������1���������ݷ��۵����ʿ�֤���ı���ADFB�������Σ��ʴ˿ɵõ�BF=AB=OC=2����CF=3-2=1�����E��F������Ϳ��������
��2���������ߵĶ�������Ϊ��1��2�����ʴ˿��������ߵĽ���ʽΪy=a��x-1��2+2��Ȼ���Ϊ����������������н�ɣ���EF������EF=PFʱ����֪E��F�������������EF�ij�����P��������ǣ�0��n�������ݹ��ɶ����Ϳ������n��ֵ���õ�P�����꣮��EF������EF=EPʱ�������ж�E��y�����̾�����EF�Ĵ�С��ϵ��ֻ�е�EF����E��y��ľ��룬P�Ŵ��ڣ���EF�ǵױ�ʱ��EP=FP�����ݹ��ɶ����Ϳ��Եõ�����n�ķ��̣��Ϳ��Խ��n��ֵ��
��3������E����x��ĶԳƵ�E�䣬����F����y��ĶԳƵ�F�䣬������Գ�ͼ�ε����ʿɵõ�NF=NF�䣬ME=ME�䣬Ȼ����������֮���߶���̿ɵõ�FN+NM+ME����Сֵ����E��F�䣬�ʴ˿ɵõ��ı���MNFE���ܳ�����Сֵ.
�����㾫����������Ĺؼ�����������κ�����ͼ������֪ʶ�����ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣬�Լ��Զ��κ��������ʵ����⣬�˽������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��

 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�