Question

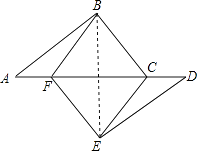
【题目】如图，点A、F、C、D在同一直线上，AB∥DE，AC=DF，AB=DE．
（1）求证：四边形BCEF是平行四边形；
（2）若∠ABC=90°，AB=8，BC=6，当AF为何值时，四边形BCEF是菱形．

Answer 1

【答案】
（1）证明：∵AB∥DE，

∴∠A=∠D，

在△BAC和△EDF中 ，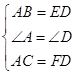

∴△BAC≌△EDF（SAS），

∴BC=EF，∠BCA=∠EFD，

∴BC∥EF，

∴四边形BCEF是平行四边形

（2）解：连接BE，交CF于点G，

∵四边形BCEF是菱形，

∴CG=FG，BE⊥AC，

∵∠ABC=90°，AB=8，BC=6，

∴AC= =10，

∵∠BGC=∠ABC=90°，∠ACB=∠BCG，

∴△ABC∽△BGC，

∴ = ，

即 = ，

∴CG=3.6，

∵FG=CG，

∴FC=2CG=7.2，

∴AF=AC﹣FC=10﹣7.2=2.8．

【解析】（1）由AB=DE，∠A=∠D，AF=DC，易证得△ABC≌DEF，即可得BC=EF，且BC∥EF，即可判定四边形BCEF是平行四边形；（2）由四边形BCEF是菱形，连接BE，交CF与点G，证得△ABC∽△BGC，由相似三角形的对应边成比例，即可求得AF的值．
【考点精析】关于本题考查的平行四边形的判定和菱形的判定方法，需要了解两组对边分别平行的四边形是平行四边形：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形；任意一个四边形，四边相等成菱形；四边形的对角线，垂直互分是菱形．已知平行四边形，邻边相等叫菱形；两对角线若垂直，顺理成章为菱形才能得出正确答案．