题目内容
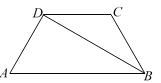
【题目】已知:如图,在梯形ABCD中,DC∥AB,AD=BC,BD平分∠ABC,∠A=60°.
求:(1)求∠CDB的度数;
(2)当AD=2时,求对角线BD的长和梯形ABCD的面积.
【答案】:(1) 30;(2)![]() .
.
【解析】分析:
(1)由已知条件易得∠ABC=∠A=60°,结合BD平分∠ABC和CD∥AB即可求得∠CDB=30°;
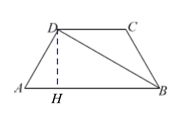
(2)过点D作DH⊥AB于点H,则∠AHD=30°,由(1)可知∠BDA=∠DBC=30°,结合∠A=60°可得∠ADB=90°,∠ADH=30°,DC=BC=AD=2,由此可得AB=2AD=4,AH=![]() ,这样即可由梯形的面积公式求出梯形ABCD的面积了.
,这样即可由梯形的面积公式求出梯形ABCD的面积了.
详解:
(1) ∵在梯形ABCD中,DC∥AB,AD=BC,∠A=60°,
∴∠CBA=∠A=60,
∵BD平分∠ABC,
∴∠CDB=∠ABD=![]() ∠CBA=30,
∠CBA=30,
(2)在△ACD中,∵∠ADB=180–∠A–∠ABD=90.
∴BD=AD ![]() A=2tan60=2
A=2tan60=2![]() .
.
过点D作DH⊥AB,垂足为H,
∴AH=AD![]() A=2sin60=
A=2sin60=![]() .
.
∵∠CDB=∠CBD=![]() ∠CBD=30,
∠CBD=30,
∴DC=BC=AD=2
∵AB=2AD=4
∴![]() .
.

练习册系列答案
相关题目