��Ŀ����
����Ŀ����������1��2019����һ�������ų��±���
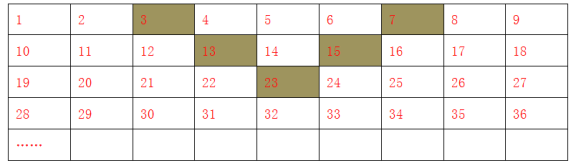
��aij��ʾ��i�е�j��������a14��4��ʾ��1�е�4������4��
��1��ֱ��д��a35�� ��a54�� ��
��2������aij��2019����ôi�� ��j�� ������i��j��ʾaij�� ��
��3���������е�5����Ӱ���ӿ���һ�����岢ƽ�ƣ������ǵ�5����֮���ܷ����2026�����ܣ� �����5�����е���С������������˵�����ɣ�
���𰸡���1��23��40����2����225��3����9��i��1��+j������9 i��9+j����3�����ܵ���2026��������.
��������
(1)���ݱ���ֱ�ӵó�����.
(2)�ٸ���ÿ����С��������8����,��2019����8,���ݳ���������������ֵ.
�ڸ��ݱ����������й��ɼ���.
(3)��5������С��Ϊx,�ú�x�Ĵ���ʽ�ֱ��ʾ������4����,������͵�ʽ�г�����,�������.
�⣺��1��a35��23��a54��40;
��2�� �١�2019��9��224��3��
��2019�ǵ�225�еĵ�3������
��i��225��j��3��
�ʴ�Ϊ225��3��
�ڸ������⣬�ɵ�aij��9��i��1��+j��
�ʴ�Ϊ9��i��1��+j������9i-9+j
��3������5�����е���С��Ϊx��������4�����ɱ�ʾΪx+4��x+10��x+12�� x+20��
�������⣬��x+x+4+x+10+x+12+x+20��2026��
���x��396��
��396��9��44��
��396�ǵ�44�еĵ�9������
����ʱx+4��400�ǵ�45�еĵ�4��������396����ͬһ�У�
�ཫ�����е�5����Ӱ���ӿ���һ�����岢ƽ�ƣ������ǵ�5����֮�Ͳ��ܵ���2026��