Question

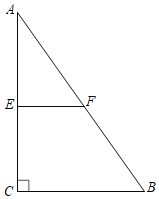
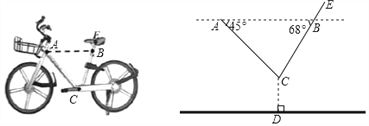
【题目】如图，有一块矩形纸片ABCD，AB=8，AD=6．将纸片折叠，使得AD边落在AB边上，折痕为AE，再将△AED沿DE向右翻折，AE与BC的交点为F，则CF的长为________

Answer 1

【答案】2

【解析】

根据折叠的性质，在第二个图中得到DB=8-6=2，∠EAD=45°；在第三个图中，得到AB=AD-DB=6-2=4，△ABF为等腰直角三角形，然后根据等腰三角形的性质和矩形的性质得到BF=AB=4，再由CF=BC-BF即可求得答案.

∵AB=8，AD=6，纸片折叠，使得AD边落在AB边上(第二个图)，

∴DB=8-6=2，∠EAD=45°，

又∵△AED沿DE向右翻折，AE与BC的交点为F(第三个图)，

∴AB=AD-DB=6-2=4，△ABF为等腰直角三角形，

∴BF=AB=4，

∴CF=BC-BF=6-4=2，

故答案为：2.