题目内容
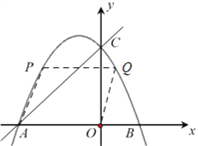
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于点A、B,与y轴交于点C,直线y=x+4经过点A、C,点P为抛物线上位于直线AC上方的一个动点.
与x轴交于点A、B,与y轴交于点C,直线y=x+4经过点A、C,点P为抛物线上位于直线AC上方的一个动点.
(1)求抛物线的表达式;
(2)如图,当CP//AO时,求∠PAC的正切值;
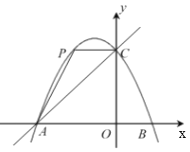
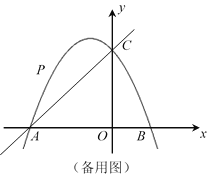
(3)当以AP、AO为邻边的平行四边形第四个顶点恰好也在抛物线上时,求出此时点P的坐标.
【答案】(1)抛物线的表达式为![]() ;(2)
;(2)![]() ;(3)P点的坐标是
;(3)P点的坐标是![]() .
.
【解析】分析:
(1)由题意易得点A、C的坐标分别为(-4,0),(0,4),将这两点坐标代入抛物线![]() 列出方程组,解得b、c的值即可求得抛物线的解析式;
列出方程组,解得b、c的值即可求得抛物线的解析式;
(2)如下图,作PH⊥AC于H,连接OP,由已知条件先求得PC=2,AC=![]() ,结合S△ABC=S△OPC,可求得PH=
,结合S△ABC=S△OPC,可求得PH=![]() ,再由OA=OC得到∠CAO=45°,结合CP∥OA可得∠PCA=45°,即可得到CH=PH=
,再由OA=OC得到∠CAO=45°,结合CP∥OA可得∠PCA=45°,即可得到CH=PH=![]() ,由此可得AH=
,由此可得AH=![]() ,这样在Rt△APH中由tan∠PAC=
,这样在Rt△APH中由tan∠PAC=![]() 即可求得所求答案了;
即可求得所求答案了;
(3)如图,当四边形AOPQ为符合要求的平行四边形时,则此时PQ=AO=4,且点P、Q关于抛物线的对称轴x=-1对称,由此可得点P的横坐标为-3,代入抛物线解析即可求得此时的点P的坐标.
详解:
(1)∵直线y=x+4经过点A、C,点A在x轴上,点C在y轴上
∴A点坐标是(﹣4,0),点C坐标是(0,4),
又∵抛物线过A,C两点,
∴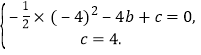
解得![]() ,
,
∴抛物线的表达式为![]() ;
;
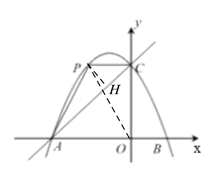
(2)作PH⊥AC于H,
∵点C、P在抛物线上,CP//AO, C(0,4),A(-4,0)
∴P(-2,4),AC=![]() ,S△ABC=S△OPC,
,S△ABC=S△OPC,
∴PC=2,![]() ,
,
∴PH=![]() ,
,
∵A(﹣4,0),C(0,4),
∴∠CAO=45°.
∵CP//AO,
∴∠ACP=∠CAO=45°,
∵PH⊥AC,
∴CH=PH=![]() ,
,
∴![]() .
.
∴![]() ;
;
(3)∵![]() ,
,
∴抛物线的对称轴为直线![]() ,
,
∵以AP,AO为邻边的平行四边形的第四个顶点Q恰好也在抛物线上,
∴PQ∥AO,且PQ=AO=4.
∵P,Q都在抛物线上,
∴P,Q关于直线![]() 对称,
对称,
∴P点的横坐标是﹣3,
∵当x=﹣3时,![]() ,
,
∴P点的坐标是![]() .
.