题目内容
【题目】如图，在平面直角坐标系中，已知△ABC的三个顶点坐标分别是A（1，1），B（4，1），C（3，3）．
（1）将△ABC向下平移5个单位后得到△A1B1C1，请画出△A1B1C1；
（2）将△ABC绕原点O逆时针旋转90°后得到△A2B2C2，请画出△A2B2C2；
（3）判断以O，A1，B为顶点的三角形的形状．（无须说明理由）
【答案】（1）画图见解析；（2）画图见解析；（3）三角形的形状为等腰直角三角形．
【解析】（1）利用点平移的坐标特征写出A1、B1、C1的坐标，然后描点即可得到△A1B1C1为所作；
（2）利用网格特定和旋转的性质画出A、B、C的对应点A2、B2、C2，从而得到△A2B2C2，
（3）根据勾股定理逆定理解答即可．
（1）如图所示，△A1B1C1即为所求；
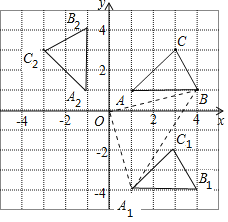
（2）如图所示，△A2B2C2即为所求；
（3）三角形的形状为等腰直角三角形，OB=OA1=
，A1B=
=
，
即OB2+OA12=A1B2，
所以三角形的形状为等腰直角三角形．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
