题目内容
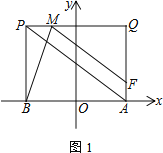
【题目】已知二次函数![]() >0)的对称轴与x轴交于点B,与直线l:
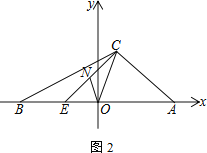
>0)的对称轴与x轴交于点B,与直线l:![]() 交于点C,点A是该二次函数图像与直线l在第二象限的交点,点D是抛物线的顶点,已知AC∶CO=1∶2,∠DOB=45°,△ACD的面积为2.
交于点C,点A是该二次函数图像与直线l在第二象限的交点,点D是抛物线的顶点,已知AC∶CO=1∶2,∠DOB=45°,△ACD的面积为2.
(1) 求抛物线的函数关系式;
(2) 若点P为抛物线对称轴上的一个点,且∠POC=45°,求点P坐标.
【答案】(1)![]() ;(2) P1(-4,12) ), P2(-4,
;(2) P1(-4,12) ), P2(-4,![]() )
)
【解析】试题分析:(1)把抛物线解析式化为顶点式,可得对称轴为直线 x=-2m,得到C的坐标,由∠DOB=45°,得到BD=BO=2m,即可得到顶点D坐标.过A作AE⊥x轴于E,可求出A的坐标,由△ACD的面积为2,得到m=2,进一步求得顶点D的坐标,从而得到抛物线的解析式;
(2)过P作PM⊥OA于M,则有PM=OM,由直线OA的解析式为:![]() ,设M(n,
,设M(n,![]() ),得到直线PM的解析式,进而得到P的坐标,因为PM=OM,由两点间的距离公式列方程,求出n的值,即可得到P的坐标.
),得到直线PM的解析式,进而得到P的坐标,因为PM=OM,由两点间的距离公式列方程,求出n的值,即可得到P的坐标.
试题解析:解:(1)![]() ,∴对称轴为直线 x=-2m,∴OB=2m,C(-2m,m).∵∠DOB=45°,∴BD=BO=2m,∴则顶点D(-2m,2m).过A作AE⊥x轴于E.∵AC:CO=1:2,∴EB:OB=1:2.∵OB=2m,∴EB=m,∴OE=3m,∴A(-3m,
,∴对称轴为直线 x=-2m,∴OB=2m,C(-2m,m).∵∠DOB=45°,∴BD=BO=2m,∴则顶点D(-2m,2m).过A作AE⊥x轴于E.∵AC:CO=1:2,∴EB:OB=1:2.∵OB=2m,∴EB=m,∴OE=3m,∴A(-3m,![]() ).∵△ACD的面积为2,∴
).∵△ACD的面积为2,∴![]() m·m=2,解得:m=±2 .∵m>0,∴m=2,∴ D(-4,4),∴
m·m=2,解得:m=±2 .∵m>0,∴m=2,∴ D(-4,4),∴![]() ,解得:a=
,解得:a=![]() ,∴
,∴![]() .
.
(2) 如图,过P作PM⊥OA于M.∵∠POC=45°,∴PM=OM.∵直线OA的解析式为:![]() ,设M(n,
,设M(n,![]() ),∴直线PM为
),∴直线PM为![]() ,即:
,即:![]() ,当x=-4时,
,当x=-4时,![]() ,∴P(-4,
,∴P(-4,![]() ).∵PM=OM,∴
).∵PM=OM,∴![]() ,解得:n=-8或n=
,解得:n=-8或n=![]() ,当n=-8时,
,当n=-8时,![]() =12,当n=
=12,当n=![]() 时,
时,![]() =
=![]() ,∴P(-4,12) )或P(-4,
,∴P(-4,12) )或P(-4,![]() ) .
) .