题目内容
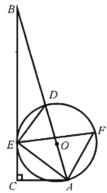
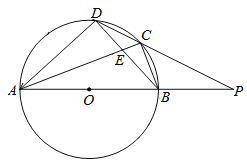
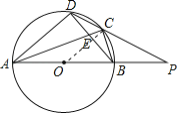
【题目】如图,在四边形ABCD中，以AB为直径的半圆O经过点C,D．AC与BD相交于点E，CD2=CE·CA,分别延长AB,DC相交于点P，PB=BO，CD=2
．则BO的长是_________．
【答案】4
【解析】
连结OC，设⊙O的半径为r，由DC2=CECA和∠ACD=∠DCE，可判断△CAD∽△CDE，得到∠CAD=∠CDE，再根据圆周角定理得∠CAD=∠CBD，所以∠CDB=∠CBD，利用等腰三角形的判定得BC=DC，证明OC∥AD，利用平行线分线段成比例定理得到
，则
，然后证明
，利用相似比得到
，再利用比例的性质可计算出r的值即可．
解：连结
，如图，设
的半径为
，
，
，
而
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，即，
，
即OB=4.
故答案为：4.
练习册系列答案
相关题目
