��Ŀ����
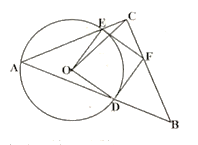
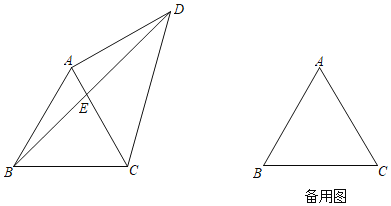
����Ŀ����ͼ����ABC�DZ߳�Ϊ2�ĵȱ������Σ���D���B�ֱ�λ��ֱ��AC�����࣬��AD��AC������BD��CD��BD��ֱ��AC�ڵ�E��
��1������CAD��90��ʱ�����߶�AE�ij���
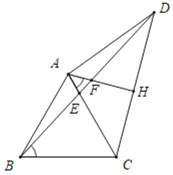
��2������A��AH��CD������Ϊ��H��ֱ��AH��BD�ڵ�F��
������CAD��120��ʱ����AE��x��y��![]() ������S��BCE��ʾ��BCE�������S��AEF��ʾ��AEF�����������y����x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��
������S��BCE��ʾ��BCE�������S��AEF��ʾ��AEF�����������y����x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��
����![]() ʱ����ֱ��д���߶�AE�ij���
ʱ����ֱ��д���߶�AE�ij���
���𰸡���1��4��2![]() ����2����y��
����2����y��![]() ��0��x��2������AE�ij�Ϊ1��
��0��x��2������AE�ij�Ϊ1��![]() ��
��
��������
��1����֤����EBC��45��������E��EG��BC������Ϊ��G��AE��x����EC��2��x������BG��EG�����������x���ɵó��𰸣�
��2����֤����AEF�ס�BEC���ɵ�![]() ���ɴ˹�����ϵʽ���ɽ�����⣮
���ɴ˹�����ϵʽ���ɽ�����⣮
�ڷ��������Σ�����CAD��120��ʱ����120������CAD��180��ʱ���ֱ�ó�������⼴��
�⣺��1���ߡ�ABC�ǵȱ������Σ�
��AB��BC��AC��2����BAC����ABC����ACB��60����
��AD��AC��
��AD��AB��
���ABD����ADB��
�ߡ�ABD+��ADB+��BAC+��CAD��180������CAD��90������ABD��15����
���EBC��45����
����E��EG��BC��������G��
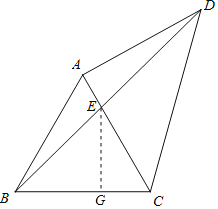
��AE��x����EC��2��x��
��Rt��CGE����ACB��60����
��EG��ECsin��ACB��![]() ��2��x����CG��ECcos��ACB��1��
��2��x����CG��ECcos��ACB��1��![]() x��
x��
��BG��2��CG��1+![]() x��
x��
��Rt��BGE����EBC��45����
��1+![]() ��2��x����
��2��x����
���x��4��2![]() ��
��
���߶�AE�ij���4��2![]() ��
��
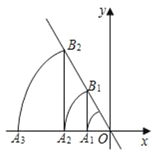
��2���ٵ���CAD��120��ʱ��
���ABD���������BDA��������DAC����BAD����BAC��120����2����
��AD��AC��AH��CD��
���CAF��![]() ��DAC��60��������
��DAC��60��������
�֡ߡ�AEF��60��+����
���AFE��60����
���AFE����ACB��
�֡ߡ�AEF����BEC��
���AEF�ס�BEC��
��![]() ��
��
�ɣ�1������Rt��CGE�У�BG��1+![]() x��EG��
x��EG��![]() ��2��x����
��2��x����
��BE2��BG2+EG2��x2��2x+4��
��y��![]() ��0��x��2����
��0��x��2����
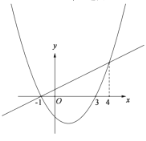
����ͼ
y��![]() ������
������![]() ��
��
������3x2+x��2��0��
���x��![]() ��1����ȥ����
��1����ȥ����
��AE��![]() ��
��
��120������CAD��180��ʱ��ͬ���ɵ�y��![]() ��
��
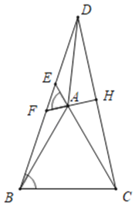
��y��![]() ʱ��
ʱ��![]() ��
��
������3x2��x��2��0��
���x����![]() ����ȥ����1��
����ȥ����1��
��AE��1��
�ۺ����Ͽɵ�AE�ij�Ϊ1��![]() ��
��

 �п�������㾫��ϵ�д�
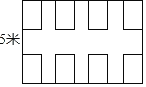
�п�������㾫��ϵ�д�����Ŀ����ͼ��ʾ����һ����5�IJ�����ֻ�ܷ�8�Ų������ּƻ�����������λ��ֻ�ܶ�ԭ���Ƚ��мӳ�����ӳ���ij���Ϊm�ף��������IJ�����Ϊy�������㣬�õ��������ݣ���ע��m��y��Ϊ��������
m���ף� | 5 | 8 | 11 | 14 | ���� |
������y���ţ� | 8 | 12 | 16 | ���� |
��1�����ݱ������ݵĹ��ɣ�������ϱ���
��2�����y����m�ĺ�������ʽ��
��3������Ҳ�������Ҫ��80�Ų�������m����Сֵ��