题目内容
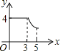
【题目】在平面直角坐标系中，抛物线y＝－
x2＋bx＋c与x轴交于点A，B，与y轴交于点C，直线y＝x＋4经过A，C两点．
(1)求抛物线的表达式；
(2)在AC上方的抛物线上有一动点P．
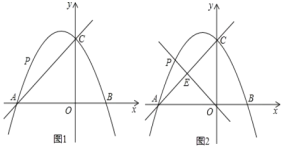
①如图1，当点P运动到某位置时，以AP，AO为邻边的平行四边形第四个顶点恰好也在抛物线上，求出此时点P的坐标；
②如图2，过点O，P的直线y＝kx交AC于点E，若PE∶OE＝3∶8，求k的值．
【答案】（1）
；（2）①
，②
或
【解析】
（1）由直线的解析式y＝x＋4易求点A和点C的坐标，把A和C的坐标分别代入y＝
x2＋bx＋c求出b和c的值即可得到抛物线的解析式；
（2）①若以AP，AO为邻边的平行四边形的第四个顶点Q恰好也在抛物线上，则PQ∥AO，再根据抛物线的对称轴可求出点P的横坐标，由（1）中的抛物线解析式，进而可求出其纵坐标，问题得解；
②过P点作PF∥OC交AC于点F，因为PF∥OC，所以△PEF∽△OEC，由相似三角形的性质：对应边的比值相等可求出PF的长，进而可设点点F（x，x＋4），利用(x2x＋4)(x＋4)＝
，可求出x的值，解方程求出x的值可得点P的坐标，代入直线y＝kx即可求出k的值．
解：(1)∵直线y＝x＋4经过A，C两点，
∴A(－4，0)，C(0，4)．
又∵抛物线过A，C两点，
∴
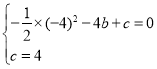解得
，
∴抛物线的表达式为y＝－x2－x＋4．
(2)①∵y＝－x2－x＋4，
∴抛物线的对称轴是直线x＝－1．
∵以AP，AO为邻边的平行四边形的第四个顶点Q恰好也在抛物线上，
∴PQ∥AO，PQ＝AO＝4
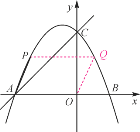
∵P，Q都在抛物线上，
∴P，Q关于直线x＝－1对称．
∴P点的横坐标是－3，
∴当x＝－3时，y＝－×(－3)2－(－3)＋4＝
∴P点的坐标是(－3，)．
②过点P作PF∥OC交AC于点F，
∵PF∥OC，
∴△PEF∽△OEC
∴
＝
又∵＝
，OC＝4，
∴PF＝
设点F(x，x＋4)，
∴P(x，－x2－x＋4)
∴(－x2－x＋4)－(x＋4)＝
解得x1＝－1，x2＝－3
∴P点坐标是(－1，
)或(－3，)．
又∵点P在直线y＝kx上，
∴k＝－或k＝－
．
