题目内容
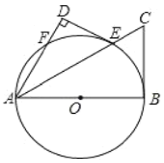
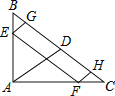
【题目】如图，在Rt△ABC中，∠BAC=90°，AB=2，AC=3，D为BC的中点，动点E，F分别在AB，AC上，分别过点EG∥AD∥FH，交BC于点G、H，若EF∥BC，则EF+EG+FH的值为（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】
先根据勾股定理计算出BC=
，再根据直角三角形斜边上的中线性质得到DA=DB=DC，则∠B=∠DAB，∠C=∠DAC，由于EF∥BC，EG∥AD∥FH，所以∠BEG=∠DAB，∠CFH=∠DAC，EF=GH，则∠B=∠BEG，∠C=∠CFH，根据等呀哦三角形的判定得BG=EG，FH=HC，所以EF+EG+FH=GH+BG+HC=BC=．
∵∠BAC=90°，AB=2，AC=3，
∴BC=
= ，
∵∠BAC=90°，D为BC的中点，
∴DA=DB=DC，
∴∠B=∠DAB，∠C=∠DAC，
∵EF∥BC，EG∥AD∥FH，
∴∠BEG=∠DAB，∠CFH=∠DAC，EF=GH，
∴∠B=∠BEG，∠C=∠CFH，
∴BG=EG，FH=HC，
∴EF+EG+FH=GH+BG+HC=BC=．
故选B．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
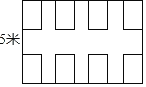
【题目】如图所示的是一个宽5米的餐厅，只能放8张餐桌．现计划扩建增加座位，只能对原宽度进行加长，设加长后的长度为m米．若餐厅的餐桌数为y，经计算，得到如下数据：（注：m和y都为正整数）
m（米） | 5 | 8 | 11 | 14 | …… |
餐桌数y（张） | 8 | 12 | 16 | …… |
（1）根据表中数据的规律，完成以上表格；
（2）求出y关于m的函数解析式；
（3）若这家餐厅至少要有80张餐桌，求m的最小值．
