题目内容
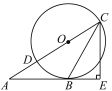
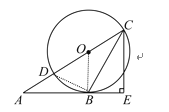
【题目】如图,CD是⊙O的直径,CB是⊙O的弦,点A在CD的延长线上,过点C作CE⊥AB,交AB的延长线于点E,且CB平分∠ACE.
(1)求证:直线AB是⊙O的切线;
(2)若BE=3,CE=4,求⊙O的半径.
【答案】(1)证明略; (2)半径为![]() .
.
【解析】
(1)连接OB,由题意可证OB∥CE,由CE⊥AE,可得OB⊥AE,则可证AB是⊙O的切线;
(2)连接BD通过△DBC∽△BEC,得到比例式![]() ,求出DC即可得结果.
,求出DC即可得结果.
解:(1)连接OB,
∵OB=OC,
∴∠OBC=∠OCB,
∵CB平分∠ACE,
∴∠OCB=∠BCE,
∴∠OBC=∠BCE,
∴OB∥CE,
∵CE⊥AE,
∴OB⊥AE,
∴直线AB是⊙O的切线;
(2)连接BD,
∵CE丄AB,
∴∠E=90°,
∴BC=![]() =5,
=5,
∵CD是⊙O的直径,
∴∠DBC=90°,
∴∠E=∠DBC,
∴△DBC∽△BEC,
∴![]()
∴BC2=DCCE,
∴DC=![]() ,
,
∴OC=![]() CD=
CD=![]() ,
,
∴⊙O的半径=![]() .
.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目