题目内容
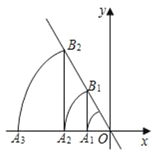
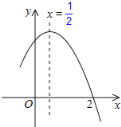
【题目】如图是二次函数y＝ax2+bx+c（a≠0）图象的一部分，对称轴x＝
，且经过点（2，0），下列说法：①abc＜0；②a+b＝0；③4a+2b+c＜0；④若（﹣
，y1），（，y2）是抛物线上的两点，则y1＞y2，其中说法正确的序号是_____
【答案】①②
【解析】
①根据抛物线开口方向、对称轴位置、抛物线与y轴交点位置求得a、b、c的符号；
②根据对称轴求出b=-a；
③把x=2代入函数关系式，结合图象判断函数值与0的大小关系；
④求出点（-
，y1）关于对称轴x=
的对称点的坐标，根据二次函数的增减性即可判断y1和y2的大小．
如图，
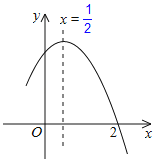
①∵二次函数的图象开口向下，
∴a＜0，
∵二次函数的图象交y轴的正半轴于一点，
∴c＞0，
∵对称轴是直线x=-
=，
∴b=-a＞0，
∴abc＜0．
故①正确；
②∵由①中知b=-a，
∴a+b=0，
故②正确；
③把x=2代入y=ax2+bx+c得：y=4a+2b+c，
∵抛物线经过点（2，0），
∴当x=2时，y=0，即4a+2b+c=0．
故③错误；
④∵（-，y1）关于对称轴x=的对称点的坐标是（
，y1），
又∵当x＞时，y随x的增大而减小，＜，
∴y1＜y2．
故④错误；
综上所述，正确的结论是①②．
故答案为：①②．
练习册系列答案
相关题目
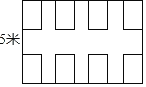
【题目】如图所示的是一个宽5米的餐厅，只能放8张餐桌．现计划扩建增加座位，只能对原宽度进行加长，设加长后的长度为m米．若餐厅的餐桌数为y，经计算，得到如下数据：（注：m和y都为正整数）
m（米） | 5 | 8 | 11 | 14 | …… |
餐桌数y（张） | 8 | 12 | 16 | …… |
（1）根据表中数据的规律，完成以上表格；
（2）求出y关于m的函数解析式；
（3）若这家餐厅至少要有80张餐桌，求m的最小值．
