Question

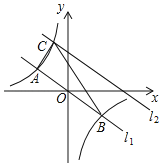
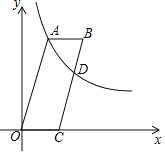
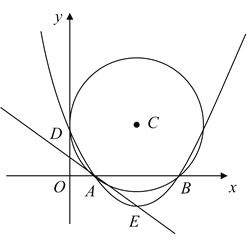
【题目】我们把方程(x- m)2+(y-n)2=r2称为圆心为(m，n)、半径长为r的圆的标准方程．例如，圆心为(1,-2)、半径长为3的圆的标准方程是(x- 1)2+(y+2)2=9．在平面直角坐标系中,圆C与轴交于点A．B．且点B的坐标为(8．0),与y轴相切于点D(0, 4)，过点A,B,D的抛物线的顶点为E．

(1)求圆C的标准方程；

(2)试判断直线AE与圆C的位置关系，并说明理由．

Answer 1

【答案】（1）；（2）相切，理由见解析

【解析】

（1）连接CD，CB，过C作CF⊥AB，分别表示出BF和CF，再在△BCF中利用勾股定理构造方程求解即可得到圆C半径以及点C坐标，从而得到标准方程；

（2）由（1）可得点A坐标，求出抛物线表达式，得到点E坐标，再求出直线AE的表达式，联立直线AE和圆C的表达式，通过判断方程根的个数即可得到两者交点个数，从而判断位置关系.

解：连接CD，CB，过C作CF⊥AB，

∵点D（0，4），B（8，0），设圆C半径为r，圆C与y轴切于点D，

则CD=BC=OF=r，CF=4，

∵CF⊥AB，

∴AF=BF=8-r，

在△BCF中，，

即，

解得：r=5，

∴CD=OF=5，即C（5，4），

∴圆C的标准方程为：；

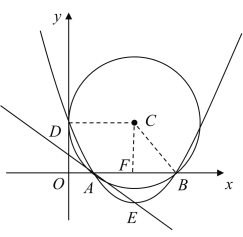
（2）由（1）可得：BF=3=AF，则OA=OB-AB=2，

即A（2，0），

设抛物线表达式为：，将A，B，D坐标代入，

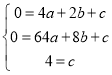，解得：，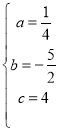

∴抛物线表达式为：，

∴可得点E（5，），

设直线AE表达式为：y=mx+n，将A和E代入，

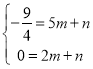可得：，解得：，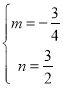

∴直线AE的表达式为：，

∵圆C的标准方程为，

联立，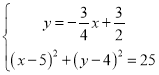

解得：x=2，

故圆C与直线AE只有一个交点，横坐标为2，

即圆C与直线AE相切.